题目内容
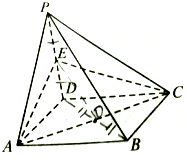如图，四棱锥P-ABCD的侧面PAD是正三角形，且垂直于底面，底面ABCD是矩形，E是PD的中点，求证：平面ACE⊥平面PCD．考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：先证明CD⊥侧面PAD，从而可得面PDC⊥侧面PAD，进而可证AE⊥平面PCD，由AE?平面ACE可证平面ACE⊥平面PCD．
解答：
证明：∵ABCD是矩形，∴CD⊥AD
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴CD⊥侧面PAD
∵CD?面PDC，∴面PDC⊥侧面PAD
正三角形PAD中，E为PD的中点，所以AE⊥PD，
∵面PDC∩面PAD=PD，∴AE⊥平面PCD．
∵AE?平面ACE
∴平面ACE⊥平面PCD
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴CD⊥侧面PAD
∵CD?面PDC，∴面PDC⊥侧面PAD
正三角形PAD中，E为PD的中点，所以AE⊥PD，
∵面PDC∩面PAD=PD，∴AE⊥平面PCD．
∵AE?平面ACE
∴平面ACE⊥平面PCD
点评：本题主要考查线面垂直的证明方法．考查学生的空间想象能力，识图的能力，严密的逻辑思维能力，属于基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
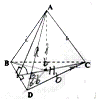如图，已知空间四边形ABCD，及两条对角线AC、BD，AB=AC=AD=a，BD=DC=CD=b，AB⊥面BCD，垂足为H，求平面ABD与平面BCD所成角的大小．
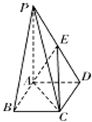如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=l，E是PD的中点．直线x+y=a 与圆x2+y2=1交于不同的两点A，B，O为坐标原点，若
•
=a，则a的值为（ ）
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|