题目内容
设C1、C2、…、Cn、…是坐标平面上的一列圆,它们的圆心都在轴的正半轴上,且都与直线y=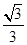 x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
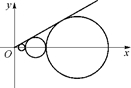
(1)证明:{rn}为等比数列;
(2)设r1=1,求数列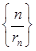 的前n项和.
的前n项和.
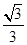 x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
(1)证明:{rn}为等比数列;
(2)设r1=1,求数列
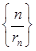 的前n项和.
的前n项和.(1)见解析(2)

(1)证明:将直线y=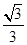 x的倾斜角记为θ,则有tanθ=
x的倾斜角记为θ,则有tanθ=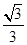 ,sinθ=
,sinθ= .
.
设Cn的圆心为(λn,0),则由题意得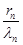 =
= ,得λn=2rn;同理λn+1=2rn+1,从而λn+1=λn+rn+rn+1=2rn+1,将λn=2rn代入,解得rn+1=3rn,故{rn}为公比q=3的等比数列.
,得λn=2rn;同理λn+1=2rn+1,从而λn+1=λn+rn+rn+1=2rn+1,将λn=2rn代入,解得rn+1=3rn,故{rn}为公比q=3的等比数列.
(2)解:由于rn=1,q=3,故rn=3n-1,从而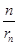 =n×31-n,
=n×31-n,
记Sn=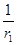 +
+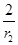 +…+
+…+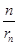 ,则有Sn=1+2×3-1+3×3-2+…+n×31-n,①
,则有Sn=1+2×3-1+3×3-2+…+n×31-n,①
 =1×3-1+2×3-2+…+(n-1)×31-n+n×3-n,②
=1×3-1+2×3-2+…+(n-1)×31-n+n×3-n,②
①-②,得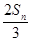 =1+3-1+3-2+…+31-n-n×3-n=
=1+3-1+3-2+…+31-n-n×3-n= -n×3-n=
-n×3-n=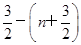 ×3-n,
×3-n,
∴Sn=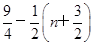 ×31-n=
×31-n= .
.
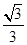 x的倾斜角记为θ,则有tanθ=
x的倾斜角记为θ,则有tanθ=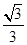 ,sinθ=
,sinθ= .
.设Cn的圆心为(λn,0),则由题意得
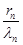 =
= ,得λn=2rn;同理λn+1=2rn+1,从而λn+1=λn+rn+rn+1=2rn+1,将λn=2rn代入,解得rn+1=3rn,故{rn}为公比q=3的等比数列.
,得λn=2rn;同理λn+1=2rn+1,从而λn+1=λn+rn+rn+1=2rn+1,将λn=2rn代入,解得rn+1=3rn,故{rn}为公比q=3的等比数列.(2)解:由于rn=1,q=3,故rn=3n-1,从而
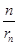 =n×31-n,
=n×31-n,记Sn=
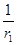 +
+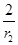 +…+
+…+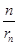 ,则有Sn=1+2×3-1+3×3-2+…+n×31-n,①
,则有Sn=1+2×3-1+3×3-2+…+n×31-n,① =1×3-1+2×3-2+…+(n-1)×31-n+n×3-n,②
=1×3-1+2×3-2+…+(n-1)×31-n+n×3-n,②①-②,得
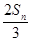 =1+3-1+3-2+…+31-n-n×3-n=
=1+3-1+3-2+…+31-n-n×3-n= -n×3-n=
-n×3-n=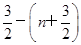 ×3-n,
×3-n,∴Sn=
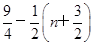 ×31-n=
×31-n= .
.
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
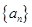 的前
的前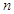 项和为
项和为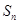 ,
,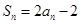 .
.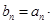 log2an+1 ,求数列
log2an+1 ,求数列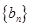 的前
的前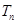 。
。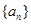 ,其前
,其前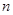 项和
项和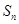 满足
满足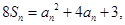 且
且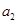 是
是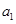 和
和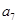 的等比中项.
的等比中项.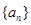 的通项公式;
的通项公式;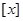 表示不超过实数
表示不超过实数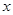 的最大整数,记
的最大整数,记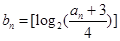 ,求
,求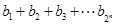 .
.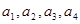 成等比数列,其公比为2,则
成等比数列,其公比为2,则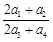 的值为( )
的值为( ) 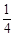
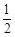
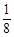
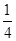 ,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.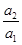 ,
,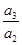 ,…,
,…,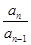 ,…是首项为1,公比为-
,…是首项为1,公比为- 的等比数列,那么a5等于( )
的等比数列,那么a5等于( )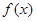 满足
满足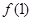 ="1" 且
="1" 且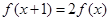 ,则
,则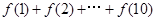 =___________.
=___________.