题目内容
已知数列{an}的前n项和为Sn,a1=1,Sn+1=4an+1,设bn=an+1-2an.证明:数列{bn}是等比数列.
见解析
由于Sn+1=4an+1,① 当n≥2时,Sn=4an-1+1.②
①-②,得an+1=4an-4an-1.
所以an+1-2an=2(an-2an-1).
又bn=an+1-2an,所以bn=2bn-1.因为a1=1,且a1+a2=4a1+1,即a2=3a1+1=4.所以b1=a2-2a1=2,故数列{bn}是首项为2,公比为2的等比数列.
①-②,得an+1=4an-4an-1.
所以an+1-2an=2(an-2an-1).
又bn=an+1-2an,所以bn=2bn-1.因为a1=1,且a1+a2=4a1+1,即a2=3a1+1=4.所以b1=a2-2a1=2,故数列{bn}是首项为2,公比为2的等比数列.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.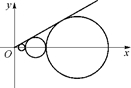
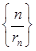 的前n项和.
的前n项和.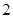 的等比数列
的等比数列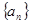 的各项都是正数,且
的各项都是正数,且 ,则
,则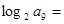 ( )
( )


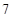
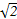 )
)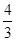 ,则{an}的前10项和为________.
,则{an}的前10项和为________.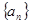 中,若
中,若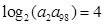 ,则
,则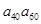 等于( )
等于( )