题目内容
(本小题满分14分)已知函数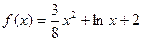 ,
,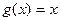 .
.
(Ⅰ)求函数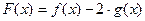 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数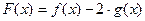 在
在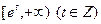 上有零点,求
上有零点,求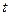 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当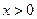 时,有
时,有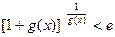 成立;若
成立;若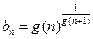 (
(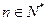 ),试问数列
),试问数列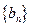 中是否存在
中是否存在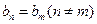 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(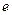 为自然对数的底数)
为自然对数的底数)
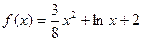 ,
,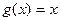 .
.(Ⅰ)求函数
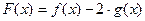 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数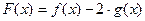 在
在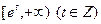 上有零点,求
上有零点,求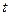 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当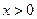 时,有
时,有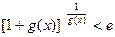 成立;若
成立;若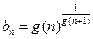 (
(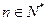 ),试问数列
),试问数列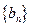 中是否存在
中是否存在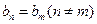 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(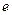 为自然对数的底数)
为自然对数的底数)(1)极大值点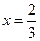 极小值点
极小值点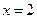 (2)
(2)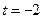 (Ⅲ)略
(Ⅲ)略
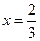 极小值点
极小值点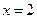 (2)
(2)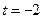 (Ⅲ)略
(Ⅲ)略:(Ⅰ)由题知: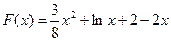 的定义域为(0,+∞)∵
的定义域为(0,+∞)∵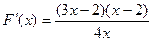

所以当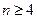 时,
时,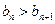 ,即:
,即: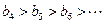 ,…12分
,…12分
又通过比较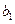 、
、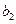 、
、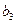 、
、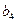 的大小知:
的大小知: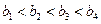 ,因为
,因为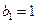 ,且
,且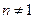 时
时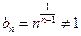 ,所以若数列
,所以若数列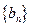 中存在相等的两项,只能是
中存在相等的两项,只能是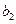 、
、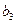 与后面的项可能相等,
与后面的项可能相等,
又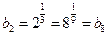 ,
,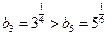 ,所以数列
,所以数列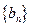 中存在唯一相等的两项,即:
中存在唯一相等的两项,即: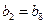 .14分
.14分
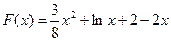 的定义域为(0,+∞)∵
的定义域为(0,+∞)∵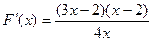

所以当
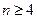 时,
时,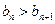 ,即:
,即: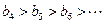 ,…12分
,…12分又通过比较
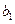 、
、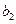 、
、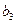 、
、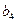 的大小知:
的大小知: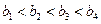 ,因为
,因为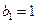 ,且
,且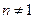 时
时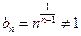 ,所以若数列
,所以若数列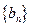 中存在相等的两项,只能是
中存在相等的两项,只能是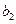 、
、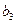 与后面的项可能相等,
与后面的项可能相等,又
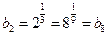 ,
,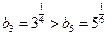 ,所以数列
,所以数列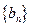 中存在唯一相等的两项,即:
中存在唯一相等的两项,即: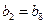 .14分
.14分
练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
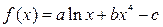 (x>0)在x = 1处取得极值
(x>0)在x = 1处取得极值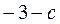 ,其中a,b,c为常数。
,其中a,b,c为常数。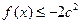 恒成立,求c的取值范围。
恒成立,求c的取值范围。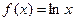 ,
, ,函数
,函数 的图象与x轴的交点也在函数
的图象与x轴的交点也在函数 的图象上,且在此点有公切线. (1)求
的图象上,且在此点有公切线. (1)求 、
、 的值;(2)对任意
的值;(2)对任意 的大小.
的大小.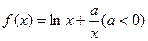 ,直线
,直线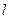 与函数
与函数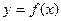 图象相切.
图象相切.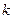 的取值范围;
的取值范围;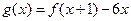 ,已知函数
,已知函数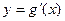 的图象经过点
的图象经过点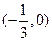 ,求函数
,求函数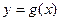 的极值.
的极值. P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明:
P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明: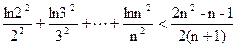 (n∈N
(n∈N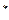 ,n≥2)
,n≥2)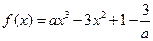 .(I)讨论函数
.(I)讨论函数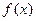 的单调性;(Ⅱ)若曲线
的单调性;(Ⅱ)若曲线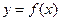 上两点A、B处的切线都与
上两点A、B处的切线都与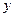 轴垂直,且线段AB与
轴垂直,且线段AB与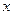 轴有公共点,求实数
轴有公共点,求实数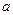 的取值范围.
的取值范围.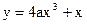 , 过点Q
, 过点Q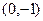 作C的切线
作C的切线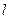 , 切点为P.
, 切点为P.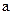 怎样变化, 点P总在一条定直线上;
怎样变化, 点P总在一条定直线上;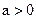 , 过点P且与
, 过点P且与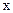 轴交于点T, 求
轴交于点T, 求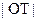 的最小值(O为原点).
的最小值(O为原点). 的导函数
的导函数 ,则数列
,则数列 的前n项和是
的前n项和是