题目内容
已知函数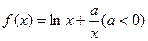 ,直线
,直线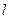 与函数
与函数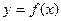 图象相切.
图象相切.
(Ⅰ)求直线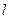 的斜率
的斜率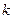 的取值范围;
的取值范围;
(Ⅱ)设函数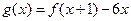 ,已知函数
,已知函数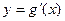 的图象经过点
的图象经过点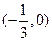 ,求函数
,求函数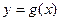 的极值.
的极值.
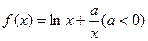 ,直线
,直线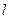 与函数
与函数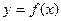 图象相切.
图象相切.(Ⅰ)求直线
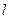 的斜率
的斜率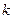 的取值范围;
的取值范围;(Ⅱ)设函数
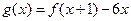 ,已知函数
,已知函数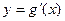 的图象经过点
的图象经过点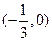 ,求函数
,求函数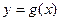 的极值.
的极值.(Ⅰ)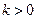 ,(Ⅱ)
,(Ⅱ)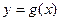 在区间
在区间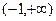 上只有极大值即
上只有极大值即
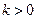 ,(Ⅱ)
,(Ⅱ)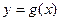 在区间
在区间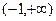 上只有极大值即
上只有极大值即
(Ⅰ)设切点坐标为 ,
,  ………………………2分
………………………2分
则 …………………………4分
…………………………4分
根据题意知: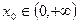 ,即
,即 ,所以
,所以
又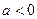 ,则
,则 ,即
,即
所以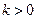 …………………………6分
…………………………6分
(Ⅱ)显然 的定义域为
的定义域为 ………7分
………7分
则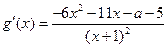 ………………………8分
………………………8分
又因为函数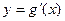 的图象经过点
的图象经过点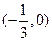 ,代入
,代入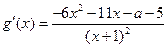
求得: ,则
,则 ……………10分
……………10分
由此可知:当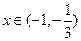 时,有
时,有 ,此时
,此时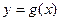 为单调增函数;
为单调增函数;
当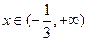 时,有
时,有 ,此时
,此时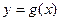 为单调减函数;
为单调减函数;
所以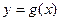 在区间
在区间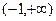 上只有极大值即
上只有极大值即 …12分
…12分
 ,
,  ………………………2分
………………………2分则
 …………………………4分
…………………………4分根据题意知:
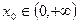 ,即
,即 ,所以
,所以
又
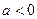 ,则
,则 ,即
,即
所以
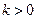 …………………………6分
…………………………6分(Ⅱ)显然
 的定义域为
的定义域为 ………7分
………7分则
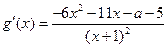 ………………………8分
………………………8分又因为函数
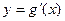 的图象经过点
的图象经过点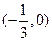 ,代入
,代入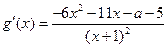
求得:
 ,则
,则 ……………10分
……………10分由此可知:当
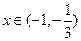 时,有
时,有 ,此时
,此时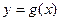 为单调增函数;
为单调增函数;当
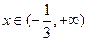 时,有
时,有 ,此时
,此时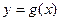 为单调减函数;
为单调减函数;所以
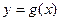 在区间
在区间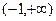 上只有极大值即
上只有极大值即 …12分
…12分
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
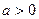 ,函数
,函数 .(1)设曲线
.(1)设曲线 在点
在点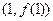 处的切线为
处的切线为 ,若
,若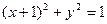 相切,求
相切,求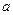 的值;(2)求函数
的值;(2)求函数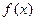 的单调区间;(3)求函数
的单调区间;(3)求函数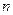 是负整数时,公式
是负整数时,公式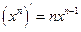 仍成立。
仍成立。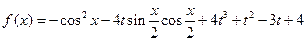 ,
,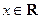 ,其中
,其中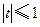 ,将
,将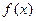 的最小值记为
的最小值记为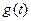 .
.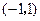 内的单调性并求极值.
内的单调性并求极值.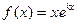 (
(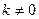 )
)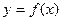 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程; 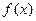 在区间(-1,1)内单调递增,求
在区间(-1,1)内单调递增,求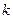 的取值范围
的取值范围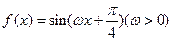 ,若
,若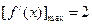 ,则
,则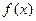 的最小正周期
的最小正周期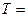 _______________.
_______________.
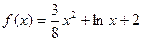 ,
,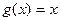 .
.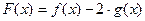 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数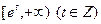 上有零点,求
上有零点,求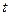 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当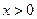 时,有
时,有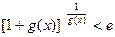 成立;若
成立;若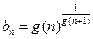 (
(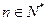 ),试问数列
),试问数列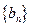 中是否存在
中是否存在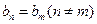 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(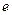 为自然对数的底数)
为自然对数的底数)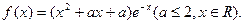
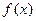 的单调区间
的单调区间

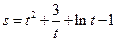 (t是时间,s是位移),则物体在时刻
(t是时间,s是位移),则物体在时刻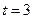 时的速度为 .
时的速度为 .