题目内容
已知曲线C: 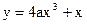 , 过点Q
, 过点Q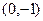 作C的切线
作C的切线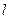 , 切点为P.
, 切点为P.
(1) 求证:不论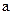 怎样变化, 点P总在一条定直线上;
怎样变化, 点P总在一条定直线上;
(2) 若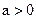 , 过点P且与
, 过点P且与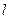 垂直的直线与
垂直的直线与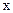 轴交于点T, 求
轴交于点T, 求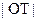 的最小值(O为原点).
的最小值(O为原点).
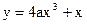 , 过点Q
, 过点Q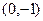 作C的切线
作C的切线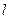 , 切点为P.
, 切点为P.(1) 求证:不论
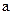 怎样变化, 点P总在一条定直线上;
怎样变化, 点P总在一条定直线上;(2) 若
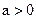 , 过点P且与
, 过点P且与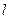 垂直的直线与
垂直的直线与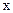 轴交于点T, 求
轴交于点T, 求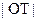 的最小值(O为原点).
的最小值(O为原点).(2)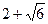
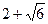
(1)设P点坐标为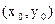 ,则
,则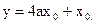 由
由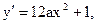 则以P点为切点的
则以P点为切点的
切线斜率为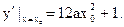 若
若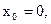 则
则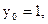 不符合题意.
不符合题意.
∵切线过点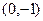 , ∴斜率为
, ∴斜率为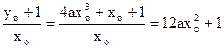 .
.
∴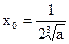 , ∴
, ∴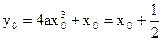 , ∴切点P总在直线
, ∴切点P总在直线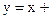
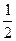 上.
上.
(2) 解法一: ∵l的斜率为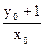 ,∴PT的斜率为
,∴PT的斜率为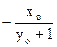 ,
,
∴PT的方程为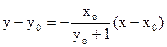 .
.
令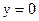 ,得PT与x轴交点的横坐标为
,得PT与x轴交点的横坐标为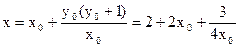 .
.
在(1)中,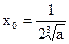 , 又
, 又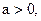 ∴
∴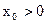 . ∴
. ∴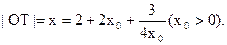
∴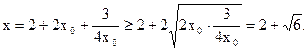
(当且仅当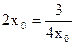 , 即
, 即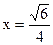 时等号成立). ∴
时等号成立). ∴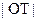 的最小值为
的最小值为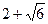 .
.
解法二:直线l的斜率为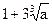 , 则垂线斜率为
, 则垂线斜率为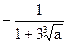 ,
,
垂线方程为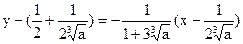 .
.
令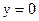 , 解得与x轴的交点T的横坐标为
, 解得与x轴的交点T的横坐标为
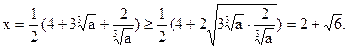
当且仅当3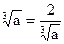 ,即
,即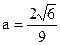 时, 等号成立.∴
时, 等号成立.∴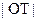 的最小值为
的最小值为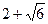 .
.
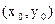 ,则
,则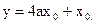 由
由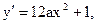 则以P点为切点的
则以P点为切点的切线斜率为
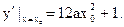 若
若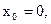 则
则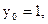 不符合题意.
不符合题意.∵切线过点
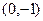 , ∴斜率为
, ∴斜率为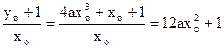 .
.∴
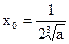 , ∴
, ∴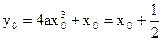 , ∴切点P总在直线
, ∴切点P总在直线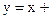
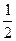 上.
上.(2) 解法一: ∵l的斜率为
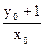 ,∴PT的斜率为
,∴PT的斜率为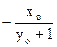 ,
,∴PT的方程为
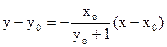 .
.令
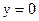 ,得PT与x轴交点的横坐标为
,得PT与x轴交点的横坐标为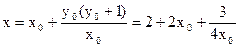 .
.在(1)中,
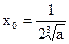 , 又
, 又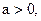 ∴
∴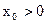 . ∴
. ∴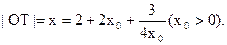
∴
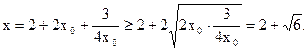
(当且仅当
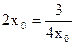 , 即
, 即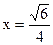 时等号成立). ∴
时等号成立). ∴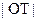 的最小值为
的最小值为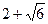 .
.解法二:直线l的斜率为
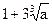 , 则垂线斜率为
, 则垂线斜率为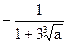 ,
,垂线方程为
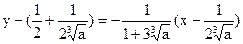 .
.令
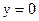 , 解得与x轴的交点T的横坐标为
, 解得与x轴的交点T的横坐标为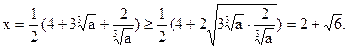
当且仅当3
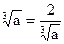 ,即
,即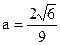 时, 等号成立.∴
时, 等号成立.∴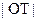 的最小值为
的最小值为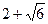 .
.
练习册系列答案
相关题目
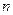 是负整数时,公式
是负整数时,公式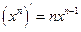 仍成立。
仍成立。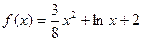 ,
,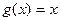 .
.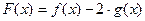 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数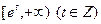 上有零点,求
上有零点,求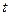 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当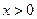 时,有
时,有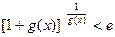 成立;若
成立;若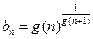 (
(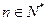 ),试问数列
),试问数列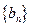 中是否存在
中是否存在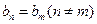 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(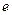 为自然对数的底数)
为自然对数的底数)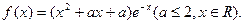
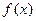 的单调区间
的单调区间

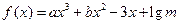 ,在
,在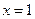 和
和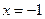 时取得极值,若对任意
时取得极值,若对任意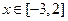 都有
都有 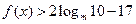 恒成立,求实数
恒成立,求实数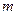 的取值集合.
的取值集合.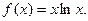 (Ⅰ)求函数
(Ⅰ)求函数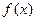 的单调区间和最小值;
的单调区间和最小值;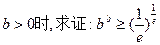 (其中e="2.718" 28…是自然对数的底数);
(其中e="2.718" 28…是自然对数的底数);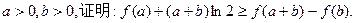
 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.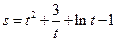 (t是时间,s是位移),则物体在时刻
(t是时间,s是位移),则物体在时刻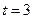 时的速度为 .
时的速度为 .