题目内容
(本小题12分)已知函数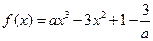 .(I)讨论函数
.(I)讨论函数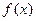 的单调性;(Ⅱ)若曲线
的单调性;(Ⅱ)若曲线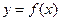 上两点A、B处的切线都与
上两点A、B处的切线都与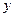 轴垂直,且线段AB与
轴垂直,且线段AB与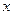 轴有公共点,求实数
轴有公共点,求实数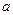 的取值范围.
的取值范围.
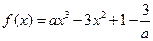 .(I)讨论函数
.(I)讨论函数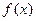 的单调性;(Ⅱ)若曲线
的单调性;(Ⅱ)若曲线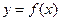 上两点A、B处的切线都与
上两点A、B处的切线都与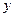 轴垂直,且线段AB与
轴垂直,且线段AB与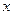 轴有公共点,求实数
轴有公共点,求实数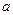 的取值范围.
的取值范围.(Ⅰ)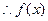 在
在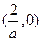 上是增函数;在
上是增函数;在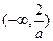 和
和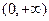 上是减函数 (Ⅱ) [-1,0)∪[3,4].
上是减函数 (Ⅱ) [-1,0)∪[3,4].
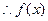 在
在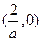 上是增函数;在
上是增函数;在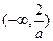 和
和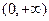 上是减函数 (Ⅱ) [-1,0)∪[3,4].
上是减函数 (Ⅱ) [-1,0)∪[3,4].由题设知 .令
.令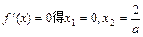 .
.
当(i)a>0时,
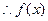 在
在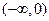 和
和 上是增函数;在
上是增函数;在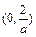 上是减函数;
上是减函数;
(i i)当a<0时,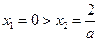
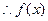 在
在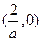 上是增函数;在
上是增函数;在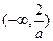 和
和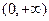 上是减函数;
上是减函数;
(Ⅱ)由(Ⅰ)的讨论及题设知,曲线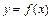 上的两点A、B的纵坐标为函数的极值,且函数
上的两点A、B的纵坐标为函数的极值,且函数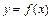 在
在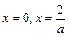 处分别是取得极值
处分别是取得极值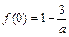 ,
,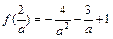 .
.
因为线段AB与x轴有公共点,所以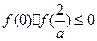 .
.
即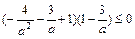 .所以
.所以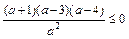 .解得 -1≤a<0或3≤a≤4.
.解得 -1≤a<0或3≤a≤4.
即所求实数a的取值范围是[-1,0)∪[3,4].
 .令
.令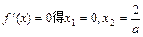 .
.当(i)a>0时,

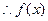 在
在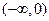 和
和 上是增函数;在
上是增函数;在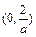 上是减函数;
上是减函数;(i i)当a<0时,
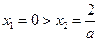
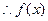 在
在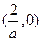 上是增函数;在
上是增函数;在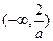 和
和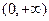 上是减函数;
上是减函数;(Ⅱ)由(Ⅰ)的讨论及题设知,曲线
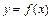 上的两点A、B的纵坐标为函数的极值,且函数
上的两点A、B的纵坐标为函数的极值,且函数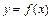 在
在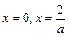 处分别是取得极值
处分别是取得极值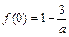 ,
,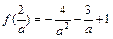 .
.因为线段AB与x轴有公共点,所以
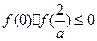 .
.即
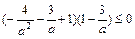 .所以
.所以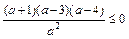 .解得 -1≤a<0或3≤a≤4.
.解得 -1≤a<0或3≤a≤4.即所求实数a的取值范围是[-1,0)∪[3,4].

练习册系列答案
相关题目
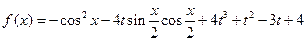 ,
,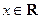 ,其中
,其中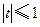 ,将
,将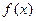 的最小值记为
的最小值记为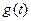 .
.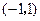 内的单调性并求极值.
内的单调性并求极值.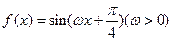 ,若
,若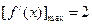 ,则
,则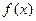 的最小正周期
的最小正周期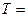 _______________.
_______________.
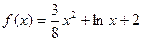 ,
,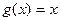 .
.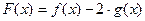 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数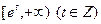 上有零点,求
上有零点,求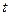 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当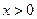 时,有
时,有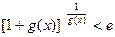 成立;若
成立;若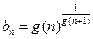 (
(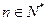 ),试问数列
),试问数列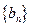 中是否存在
中是否存在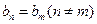 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(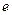 为自然对数的底数)
为自然对数的底数)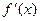 <0,设a="f(0),b=" f(
<0,设a="f(0),b=" f(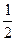 ),c= f(3),则 ( )
),c= f(3),则 ( )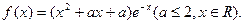
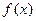 的单调区间
的单调区间

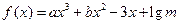 ,在
,在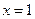 和
和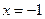 时取得极值,若对任意
时取得极值,若对任意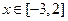 都有
都有 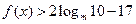 恒成立,求实数
恒成立,求实数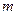 的取值集合.
的取值集合. ,若
,若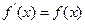 ,则
,则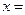 。
。