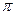题目内容
(12分)设函数f(x)=lnx-px+1(1)当 P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明:
P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明: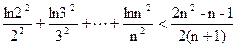 (n∈N
(n∈N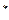 ,n≥2)
,n≥2)
 P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明:
P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明: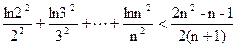 (n∈N
(n∈N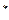 ,n≥2)
,n≥2)(1)P≥ 1(2)
1(2)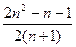
 1(2)
1(2)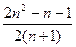
:(1)f(x)=ln2x-px+1定义域(0,+∞),f′(x)=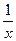 -p=
-p=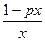 =
=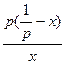
当P>0时,令f′(x)=0,x=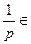 (0,+∞)…………3分
(0,+∞)…………3分
当x∈(0,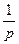 )时,f′(x)>0 f(x)
)时,f′(x)>0 f(x) 为增函数,
为增函数,
当x∈(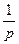 ,+∞)时f′(x)<0 f(x)为减函数。f(x)max=f(
,+∞)时f′(x)<0 f(x)为减函数。f(x)max=f(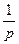 )=ln
)=ln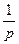
要使f(x)≤0恒成立只要f(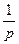 )=ln
)=ln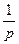 ≤0∴P≥
≤0∴P≥ 1………5分
1………5分
(2)令P="1" 由(1)知:lnx-x+1≤0∴lnx≤x-1 n≥2
lnn2≤n2-1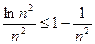 ………8分
………8分
∴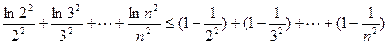
=(n-1)-(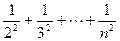 )<(n-1)-[
)<(n-1)-[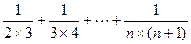 ]
]
=(n-1)-(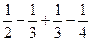 +
+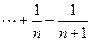 )=(n-1)-(
)=(n-1)-(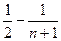 )=
)=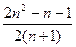 …12分
…12分
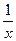 -p=
-p=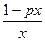 =
=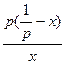
当P>0时,令f′(x)=0,x=
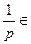 (0,+∞)…………3分
(0,+∞)…………3分当x∈(0,
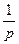 )时,f′(x)>0 f(x)
)时,f′(x)>0 f(x) 为增函数,
为增函数,当x∈(
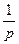 ,+∞)时f′(x)<0 f(x)为减函数。f(x)max=f(
,+∞)时f′(x)<0 f(x)为减函数。f(x)max=f(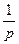 )=ln
)=ln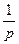
要使f(x)≤0恒成立只要f(
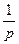 )=ln
)=ln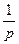 ≤0∴P≥
≤0∴P≥ 1………5分
1………5分(2)令P="1" 由(1)知:lnx-x+1≤0∴lnx≤x-1 n≥2
lnn2≤n2-1
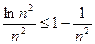 ………8分
………8分∴
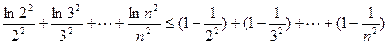
=(n-1)-(
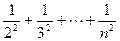 )<(n-1)-[
)<(n-1)-[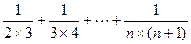 ]
]=(n-1)-(
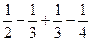 +
+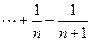 )=(n-1)-(
)=(n-1)-(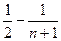 )=
)=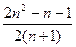 …12分
…12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
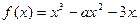 (1)若
(1)若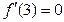 ,求
,求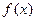 在
在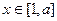 上的最小值和最大值.(2)若
上的最小值和最大值.(2)若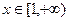 上是增函数,求:实数a的取值范围;
上是增函数,求:实数a的取值范围;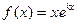 (
(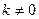 )
)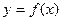 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程; 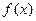 在区间(-1,1)内单调递增,求
在区间(-1,1)内单调递增,求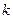 的取值范围
的取值范围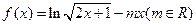 .
.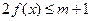 恒成立,求
恒成立,求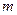 的取值范围.
的取值范围.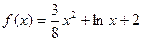 ,
,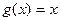 .
.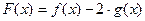 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数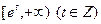 上有零点,求
上有零点,求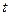 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当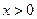 时,有
时,有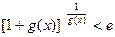 成立;若
成立;若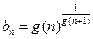 (
(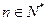 ),试问数列
),试问数列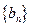 中是否存在
中是否存在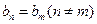 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(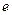 为自然对数的底数)
为自然对数的底数)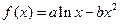 图象上一点
图象上一点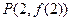 处的切线方程为
处的切线方程为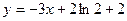 .
.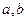 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在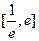 内有两个不等实根,求
内有两个不等实根,求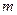 的取值范围(其中
的取值范围(其中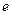 为自然对数的底数,
为自然对数的底数,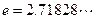 );
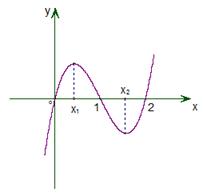
); 的大致图象,则
的大致图象,则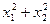 等于( )
等于( )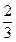
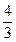
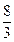
 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点. 等于( )
等于( )