Question

【题目】给定直线m：y=2x－16，抛物线C：y2=ax（a>0）.

（1）当抛物线C的焦点在直线m上时，确定抛物线C的方程；

（2）若△ABC的三个顶点都在（1）所确定的抛物线C上，且点A的纵坐标y=8，△ABC的重心恰在抛物线C的焦点上，求直线BC的方程．

Answer 1

【答案】（1）；（2）．

【解析】

试题（1）由抛物线的标准方程可得其焦点为，它在直线上，代入可得值；（2）由已知点坐标为，焦点为，因此由重心坐标公式得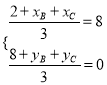，从而有，故得出中点坐标为，的斜率求法是：把坐标代入抛物线方程，所得两式相减（点差法）可得．

试题解析：（1）∵抛物线的焦点为（，0），代入y=2x-16，得a=32．

∴抛物线方程为y2=32x．

（2）∵yA=8，∴xA=2.

∵F（8，0）为△ABC的重心，∴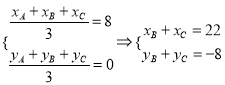

又（yB+yC）（yB-yC）=32（xB-xC）=-4=kBC，

又中线AF与BC交点坐标x==11，y===-4，

∴BC的直线方程为y+4=-4（x-11），即4x+y-40=0．