题目内容
在直角坐标系中,直线l:x-
y-2=0被以原点为极点,x轴正半轴的极坐标方程ρ=2cosθ的曲线C所截,则所截得的弦长为 .
| 3 |
考点:简单曲线的极坐标方程
专题:直线与圆,坐标系和参数方程
分析:先将圆的极坐标方程化成直角坐标下的标准方程,求出圆心坐标和半径,利用点到直线的距离公式求出圆心到直线l的距离,利用弦长公式即可求出截得的弦长.
解答:
解:由ρ=2cosθ得,ρ2=2ρcosθ,则x2+y2=2x,
所以曲线C的标准方程是(x-1)2+y2=1,
则曲线C是以(1,0)为圆心、半径为1的圆,
所以(1,0)到直线l的距离d=
=
,
则所截得的弦长为:2
=
,
故答案为:
.
所以曲线C的标准方程是(x-1)2+y2=1,
则曲线C是以(1,0)为圆心、半径为1的圆,
所以(1,0)到直线l的距离d=
| |1-2| |
| 2 |
| 1 |
| 2 |
则所截得的弦长为:2
1-(
|
| 3 |
故答案为:
| 3 |
点评:本题主要考查简单曲线的极坐标方程化成直角坐标方程,点到直线的距离公式,以及直线被圆所截得的弦长公式等知识,熟练掌握公式是解题的关键.

练习册系列答案
相关题目
要得到函数y=cos(2x-
)的图象,只需将函数y=cos(2x+
)的图象( )
| 2π |
| 3 |
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
(文)现有四个函数:①y=x•sinx;②y=x•cosx;③y=x|cosx|;④y=x•2x的图象(部分)如图:

则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
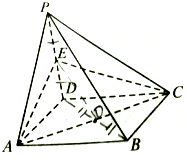 如图,四棱锥P-ABCD的侧面PAD是正三角形,且垂直于底面,底面ABCD是矩形,E是PD的中点,求证:平面ACE⊥平面PCD.
如图,四棱锥P-ABCD的侧面PAD是正三角形,且垂直于底面,底面ABCD是矩形,E是PD的中点,求证:平面ACE⊥平面PCD.