题目内容
是否存在同时满足以下条件的复数z1，z2；
（1）
=0；（2）
=
+6；（3）z1z22+z2+2=0，如果不存在说明理由；如果存在，请求出z1和z2．
（1）
z1-
| ||
z2-
|
| 2 |
| z2+6 |
. |
| z2 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由（1）可得z1 是实数，z2不是实数，可设z1=a，且a∈R，z2=c+di，c、d∈R，d≠0．由（2），可得 c2+d2+12c=-34．由（3）可得 ac2-ad2+c+2=0，且2cd+d=0．解方程组可得d无解，可得不存在同时满足条件的复数z1，z2．
解答：
解：由（1）
=0 可得z1=
，且z2≠
，故z1 是实数，z2不是实数，
故可设z1=a，且a∈R，z2=c+di，c、d∈R，d≠0．
由（2）
=
+6，可得|z2|2+6（z2+
）=-34，即 c2+d2+12c=-34．
由（3）z1z22+z2+2=0，可得a（c2-d2+2cdi ）+c+di+2=0，即 ac2-ad2+c+2+（2cd+d）i=0，
∴ac2-ad2+c+2=0，2cd+d=0．
解得c=-
，d2=-
，故d不存在，故不存在同时满足条件的复数z1，z2．
z1-
| ||
z2-
|
. |
| z1 |
. |
| z2 |
故可设z1=a，且a∈R，z2=c+di，c、d∈R，d≠0．
由（2）
| 2 |
| z2+6 |
. |
| z2 |
. |
| z2 |
由（3）z1z22+z2+2=0，可得a（c2-d2+2cdi ）+c+di+2=0，即 ac2-ad2+c+2+（2cd+d）i=0，
∴ac2-ad2+c+2=0，2cd+d=0．
解得c=-
| 1 |
| 2 |
| 113 |
| 4 |
点评：本题主要考查两个复数代数形式的乘除法法则的应用，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
相关题目
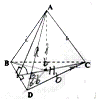如图，已知空间四边形ABCD，及两条对角线AC、BD，AB=AC=AD=a，BD=DC=CD=b，AB⊥面BCD，垂足为H，求平面ABD与平面BCD所成角的大小．