题目内容
平行四边形ABCD中,
=
B
,
=
,
=
,
=
,若
=
+
,求m-n的值.
| BM |
| 2 |
| 3 |
| BD |
| CN |
| 1 |
| 4 |
| CA |
| AB |
| a |
| AD |
| b |
| MN |
| ma |
| nb |
考点:向量的加法及其几何意义,向量的减法及其几何意义
专题:计算题,作图题,平面向量及应用
分析:如图,可化出
=
(-
-
);
=
(
-
);从而求
=
+
,从而求得m,n.
| NO |
| 1 |
| 4 |
| a |
| b |
| OM |
| 1 |
| 6 |
| b |
| a |
| MN |
| 5 |
| 12 |
| a |
| 1 |
| 12 |
| b |
解答:
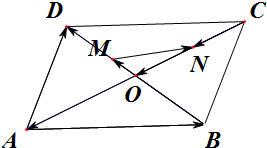 解:如图,
解:如图,
=
=
=
(
+
)
=
(-
-
)=
(-
-
);
=
-
=
-
=
=
(
-
)=
(
-
);
故
=
+
=-(
+
)
=-[
(
-
)+
(-
-
)]
=
+
=
+
;
故m=
,n=
;
故m-n=
.
 解:如图,
解:如图,| NO |
| CN |
| 1 |
| 4 |
| CA |
| 1 |
| 4 |
| CB |
| BA |
=
| 1 |
| 4 |
| AD |
| AB |
| 1 |
| 4 |
| a |
| b |
| OM |
| BM |
| BO |
| 2 |
| 3 |
| BD |
| 1 |
| 2 |
| BD |
| 1 |
| 6 |
| BD |
=
| 1 |
| 6 |
| AD |
| AB |
| 1 |
| 6 |
| b |
| a |
故
| MN |
| MO |
| ON |
=-(
| OM |
| NO |
=-[
| 1 |
| 6 |
| b |
| a |
| 1 |
| 4 |
| a |
| b |
=
| 5 |
| 12 |
| a |
| 1 |
| 12 |
| b |
| ma |
| nb |
故m=
| 5 |
| 12 |
| 1 |
| 12 |
故m-n=
| 1 |
| 3 |
点评:本题考查了平面向量的线性运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线x+y=a 与圆x2+y2=1交于不同的两点A,B,O为坐标原点,若
•
=a,则a的值为( )
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1的一个焦点在圆x2+y2-4x-5=0上,则双曲线的离心率为( )
| x2 |
| 9 |
| y2 |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
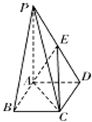 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=l,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=l,E是PD的中点.