题目内容
9.在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,离心率为$\frac{{\sqrt{3}}}{3}$,直线l:x=3为椭圆的一条准线.(1)求椭圆的方程;
(2)若$C(\sqrt{3},\sqrt{,3})$,$D(-\sqrt{3},\sqrt{,3})$,Q为椭圆上位于x轴上方的动点,直线DM•CN,BQ分别交直线m于点M,N.
(i)当直线AQ的斜率为$\frac{1}{2}$时,求△AMN的面积;
(ii)求证:对任意的动点Q,DM•CN为定值.
分析 (1)通过椭圆的性质计算即可;
(2)通过(1)知$A(-\sqrt{3},0)$,$B(\sqrt{3},0)$,$M(\frac{{\sqrt{3}{x_0}-\sqrt{3}{y_0}+3}}{y_0},\sqrt{3})$,$N(\frac{{\sqrt{3}{x_0}+\sqrt{3}{y_0}-3}}{y_0},\sqrt{3})$.(i)通过直线AQ的斜率为$\frac{1}{2}$并与椭圆方程联立,可得M、N点坐标,利用三角形面积公式计算即可;(ii)利用两点间距离公式计算即可.
解答 解: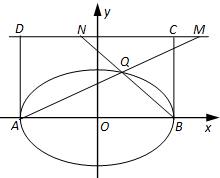 (1)由题意知,$\left\{\begin{array}{l}\frac{a^2}{{\sqrt{{a^2}-{b^2}}}}=3\\ \frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{3}\end{array}\right.$,解得$\left\{\begin{array}{l}a=\sqrt{3}\\{b^2}=2\end{array}\right.$,
(1)由题意知,$\left\{\begin{array}{l}\frac{a^2}{{\sqrt{{a^2}-{b^2}}}}=3\\ \frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{3}\end{array}\right.$,解得$\left\{\begin{array}{l}a=\sqrt{3}\\{b^2}=2\end{array}\right.$,
故椭圆的方程为$\frac{x^2}{3}+\frac{y^2}{2}=1$;
(2)由(1)知$A(-\sqrt{3},0)$,$B(\sqrt{3},0)$,
设Q(x0,y0),y0>0,
则$2{x_0}^2+3{y_0}^2=6$,直线AQ的方程为$y=\frac{y_0}{{{x_0}+\sqrt{3}}}(x+\sqrt{3})$,
令$y=\sqrt{3}$,得$M(\frac{{\sqrt{3}{x_0}-\sqrt{3}{y_0}+3}}{y_0},\sqrt{3})$,
直线BQ的方程为$y=\frac{y_0}{{{x_0}-\sqrt{3}}}(x-\sqrt{3})$,
令$y=\sqrt{3}$,得$N(\frac{{\sqrt{3}{x_0}+\sqrt{3}{y_0}-3}}{y_0},\sqrt{3})$.
(i)当直线AQ的斜率为$\frac{1}{2}$时,有$\left\{\begin{array}{l}\frac{y_0}{{{x_0}+\sqrt{3}}}=\frac{1}{2}\\ 2{x_0}^2+3{y_0}^2=6\end{array}\right.$,
消去x0并整理得,$11{y_0}^2-8\sqrt{3}{y_0}=0$,
解得${y_0}=\frac{{8\sqrt{3}}}{11}$或y0=0(舍),
∴△AMN的面积${S_{△AMN}}=\frac{{\sqrt{3}}}{2}×MN=\frac{{\sqrt{3}}}{2}×|{\frac{{\sqrt{3}{x_0}-\sqrt{3}{y_0}+3}}{y_0}-\frac{{\sqrt{3}{x_0}+\sqrt{3}{y_0}-3}}{y_0}}|$=$3×|{\frac{{\sqrt{3}-{y_0}}}{y_0}}|$=$\frac{9}{8}$;
(ii)证明:$DM=|{\frac{{\sqrt{3}{x_0}-\sqrt{3}{y_0}+3}}{y_0}+\sqrt{3}}|=|{\frac{{\sqrt{3}{x_0}+3}}{y_0}}|$,
$CN=|{\frac{{\sqrt{3}{x_0}+\sqrt{3}{y_0}-3}}{y_0}-\sqrt{3}}|=|{\frac{{\sqrt{3}{x_0}-3}}{y_0}}|$,
∴$DM•CN=|{\frac{{\sqrt{3}{x_0}+3}}{y_0}}|•|{\frac{{\sqrt{3}{x_0}-3}}{y_0}}|=|{\frac{{3{x_0}^2-9}}{{{y_0}^2}}}|=|{\frac{{3{x_0}^2-9}}{{\frac{{6-2{x_0}^2}}{3}}}}|=\frac{9}{2}$,
所以对任意的动点Q,DM•CN为定值,该定值为$\frac{9}{2}$.
点评 本题是一道关于椭圆的综合题,涉及到两点间距离公式、三角形面积公式等基础知识,注意解题方法的积累,属于中档题.

| A. | 720种 | B. | 48种 | C. | 96种 | D. | 192种 |
| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{5}{9}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
