题目内容
18.函数f(x)=|x-3|(${2^{sin\frac{πx}{2}}}$-1)-1(-3≤x≤9)的所有零点之和为( )| A. | 6 | B. | 10 | C. | 12 | D. | 18 |
分析 作函数y=${2^{sin\frac{πx}{2}}}$-1与函数y=$\frac{1}{|x-3|}$在[-3,9]上的图象如下,从而结合图象求解零点之和.
解答 解:令|x-3|(${2^{sin\frac{πx}{2}}}$-1)-1=0,
${2^{sin\frac{πx}{2}}}$-1=$\frac{1}{|x-3|}$,(x≠3);
作函数y=${2^{sin\frac{πx}{2}}}$-1与函数y=$\frac{1}{|x-3|}$在[-3,9]上的图象如下,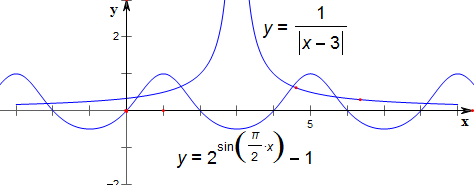
结合图象可知,
函数y=${2^{sin\frac{πx}{2}}}$-1与函数y=$\frac{1}{|x-3|}$在[-3,9]上关于x=3对称;
函数y=${2^{sin\frac{πx}{2}}}$-1与函数y=$\frac{1}{|x-3|}$在[-3,9]上有6个交点;
故函数f(x)=|x-3|(${2^{sin\frac{πx}{2}}}$-1)-1(-3≤x≤9)的所有零点之和为3×6=18;
故选D.
点评 本题考查了函数的性质的应用及数形结合的思想应用,属于基础题.

练习册系列答案
相关题目
6. 正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
 正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )| A. | $\sqrt{5}$+$\sqrt{6}$ | B. | 2$\sqrt{5}$+2$\sqrt{6}$ | C. | $\sqrt{5}$+$\frac{{\sqrt{6}}}{2}$ | D. | 2$\sqrt{5}$+$\sqrt{6}$ |
3.已知点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,则(a-m)2+(b-n)2的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 8 |
10.在等差数列{an}中,若2a3+a9=33,则数列{an}的前9项和等于( )
| A. | 95 | B. | 100 | C. | 99 | D. | 90 |
8.已知sin(π-α)=-2sin($\frac{π}{2}+α$),则$\frac{sinα+cosα}{sinα-cosα}$等于( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |