题目内容

12．学校举行数学模块考试，最后一个考场只有6名学生，其中有4名文科生和2名理科生，要求把这6名学生排成一列，最后一名必须是理科生，且2名理科生不能相邻，则教务员安排考场时不同的安排方法有（　　）
A．720种B．48种C．96种D．192种

分析 先排最后一名，再排倒数第二名，最后排其它，根据分步计数原理即可得到答案．

解答 解：先排最后一名，从2名理科生选择一名，
再排倒数第二名，从4名文科生选择一名，
最后剩下的4名同学任意排，
根据分步计数原理，故有${C}_{2}^{1}•{C}_{4}^{1}•{A}_{4}^{4}$=192种．
故选：D．

点评 本题考查了分步计数原理，关键是特殊元素特殊安排，属于基础题．

练习册系列答案
相关题目
2．已知cosα=$\frac{3}{5}$，则sin（$\frac{π}{2}$-α）=（　　）
A．$\frac{3}{5}$B．-$\frac{3}{5}$C．$\frac{4}{5}$D．-$\frac{4}{5}$
3．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=4，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，则$\overrightarrow{a}$•$\overrightarrow{b}$的值是（　　）
A．2B．±2C．4D．±4
20．已知函数f（x）=2sin（ωx+θ ） （ω＞0）的图象如图所示，则ω=2，若将函数f（x）的图象向左平移φ $（{0＜φ＜\frac{π}{2}}）$个单位后得到一个偶函数，则φ=$\frac{π}{3}$．
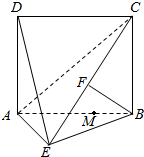7．如图，四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点．且BF⊥平面ACE．
（1）求证：平面ADE⊥平面BCE；
（2）求二面角E-AC-B的大小；
（3）设M在线段AB上，且满足AM=2MB，试在线段CE上确定一点N，使得MN∥平面DAE．
17．若x∈[-$\frac{5π}{12}$，-$\frac{π}{3}$]，则y=tan（x+$\frac{2π}{3}$）-tan（x+$\frac{π}{6}$）+cos（x+$\frac{π}{6}$）的最大值是$\frac{11\sqrt{3}}{6}$．
4．已知sin（$\frac{π}{4}$+α）=$\frac{1}{3}$，α是第二象限角，则sin（2α+$\frac{5π}{6}$）=$\frac{4\sqrt{2}-7\sqrt{3}}{18}$或-$\frac{7\sqrt{3}+4\sqrt{2}}{18}$．
1．在等差数列{an}中，若2（a3+a4+a5）+3（a9+a11）=42，则S13=26．
9．在平面直角坐标系xOy中，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点分别为A，B，离心率为$\frac{{\sqrt{3}}}{3}$，直线l：x=3为椭圆的一条准线．
（1）求椭圆的方程；
（2）若$C（\sqrt{3}，\sqrt{，3}）$，$D（-\sqrt{3}，\sqrt{，3}）$，Q为椭圆上位于x轴上方的动点，直线DM•CN，BQ分别交直线m于点M，N．
（i）当直线AQ的斜率为$\frac{1}{2}$时，求△AMN的面积；
（ii）求证：对任意的动点Q，DM•CN为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网