题目内容
4.椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1上一点P到一个焦点的距离为5,则P到另一个焦点的距离为( )| A. | 10 | B. | 6 | C. | 5 | D. | 4 |
分析 求出椭圆的a,b,c,再由椭圆的定义,即可得到所求距离.
解答 解:椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1的a=5,b=3,
c=$\sqrt{{a}^{2}-{b}^{2}}$=3,
即有焦点F(-3,0),F'(3,0),
由椭圆的定义,可得
|PF|+|PF'|=2a=10,
由题意可得,设|PF|=5,
则|PF'|=5.
故选:C.
点评 本题考查椭圆的方程和性质,主要考查椭圆的定义,考查运算能力,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12. 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )| A. | ($\frac{1}{3}$,$\frac{{\sqrt{2}}}{2}$] | B. | (0,$\frac{5}{7}$] | C. | [$\frac{5}{7}$,1) | D. | ($\frac{1}{3}$,$\frac{5}{7}$] |
16.椭圆$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1的焦距为( )
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 4 |
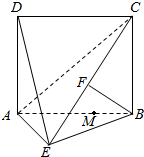 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.