题目内容
13.如图所示,直线m∥n,AB⊥m,∠ABC=130°,那么∠α为40°.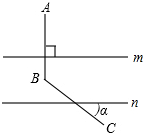
分析 延长AB交直线n于E,求出∠AED=90°,根据三角形的外角性质 求出∠BDE即可.
解答 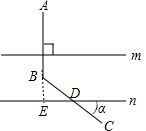 解:如图,延长AB交直线n于E,
解:如图,延长AB交直线n于E,
∵直线m∥n,AB⊥m,
∴AE⊥直线n,
∴∠AED=90°,
∵∠ABC=130°,
∴∠BDE=130°-90°=40°,
即∠α=40°,
故答案为:40°.
点评 本题考查了平行线的性质和判定,三角形外角性质的应用,解此题的关键是求出∠BDE的度数,注意:两直线平行,同位角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12. 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )| A. | ($\frac{1}{3}$,$\frac{{\sqrt{2}}}{2}$] | B. | (0,$\frac{5}{7}$] | C. | [$\frac{5}{7}$,1) | D. | ($\frac{1}{3}$,$\frac{5}{7}$] |
10.在等差数列{an}中,若2a3+a9=33,则数列{an}的前9项和等于( )
| A. | 95 | B. | 100 | C. | 99 | D. | 90 |
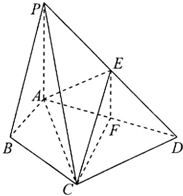 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°.