题目内容
已知抛物线 直线
直线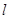 过抛物线的焦点
过抛物线的焦点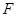 且与该抛物线交于
且与该抛物线交于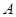 、
、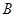 两点(点A在第一象限)
两点(点A在第一象限)
(Ⅰ)若 ,求直线
,求直线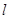 的方程;
的方程;
(Ⅱ)过点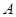 的抛物线的切线与直线
的抛物线的切线与直线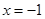 交于点
交于点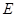 ,求证:
,求证: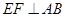 。
。
 直线
直线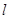 过抛物线的焦点
过抛物线的焦点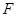 且与该抛物线交于
且与该抛物线交于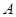 、
、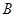 两点(点A在第一象限)
两点(点A在第一象限) (Ⅰ)若
 ,求直线
,求直线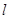 的方程;
的方程;(Ⅱ)过点
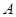 的抛物线的切线与直线
的抛物线的切线与直线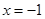 交于点
交于点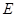 ,求证:
,求证: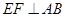 。
。(Ⅰ)解:设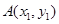 ,
,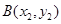 若
若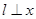 轴,则
轴,则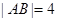 不适合
不适合
故设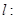
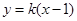 ,代入抛物线方程得
,代入抛物线方程得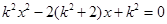
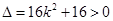
由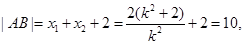 得
得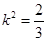 直线
直线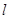 的方程为
的方程为
(Ⅱ)当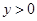 时
时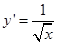 切线的方程:
切线的方程: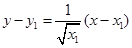 得
得
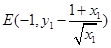
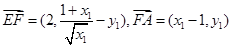
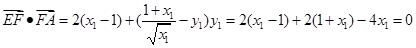
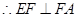 即
即 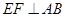
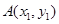 ,
,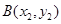 若
若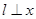 轴,则
轴,则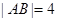 不适合
不适合故设
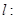
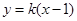 ,代入抛物线方程得
,代入抛物线方程得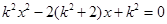
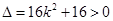
由
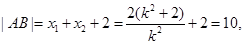 得
得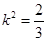 直线
直线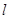 的方程为
的方程为
(Ⅱ)当
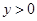 时
时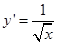 切线的方程:
切线的方程: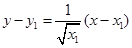 得
得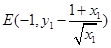
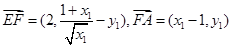
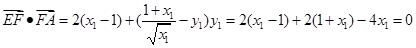
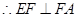 即
即 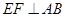
本试题主要是考查了直线与抛物线的位置关系,利用联立方程组,结合韦达定理求解弦长和直线的方程,以及证明垂直问题。

练习册系列答案
相关题目
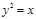 上的点到直线
上的点到直线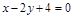 的距离最小的点的坐标是 .
的距离最小的点的坐标是 . 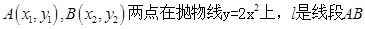 的垂直平分线.
的垂直平分线.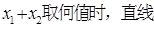
 ?
? 轴上截距的取值范围.
轴上截距的取值范围.  的焦点
的焦点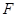 的直线
的直线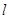 交
交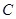 于
于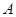 、
、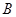 两点(点
两点(点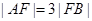 ,则
,则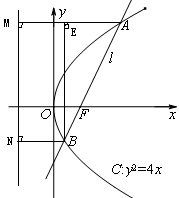
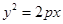 的焦点
的焦点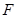 与双曲线
与双曲线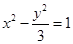 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与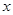 轴的交点为
轴的交点为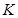 ,点
,点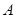 在抛物线上且
在抛物线上且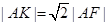 ,则
,则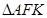 的面积为( )
的面积为( )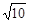 时, 求k的值.
时, 求k的值.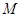 到点
到点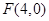 的距离比它到定直线
的距离比它到定直线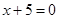 的距离小1,则点
的距离小1,则点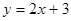 与抛物线
与抛物线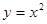 所围成的图形面积是
所围成的图形面积是