题目内容
已知抛物线 y 2 =" –" x与直线 y =" k" ( x + 1 )相交于A、B两点, 点O是坐标原点.
(1) 求证: OA^OB;
(2) 当△OAB的面积等于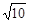 时, 求k的值.
时, 求k的值.
(1) 求证: OA^OB;
(2) 当△OAB的面积等于
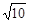 时, 求k的值.
时, 求k的值.解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意, ………… 2分
∴k ¹ 0由y =" k" (x+1)得x =
 –1 代入y 2 =" –" x 整理得: y 2 +
–1 代入y 2 =" –" x 整理得: y 2 +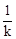 y – 1 =" 0" , 2分
y – 1 =" 0" , 2分设A (x 1 , y 1), B (x 2 , y 2) 则y 1 + y 2 = –
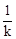 , y 1y 2 =" –1." ………… 2分
, y 1y 2 =" –1." ………… 2分∵A、B在y 2 =" –" x上, ∴A (–
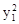 , y 1 ), B (–
, y 1 ), B (– , y 2 ) ,
, y 2 ) ,∴ kOA·kOB =
 =
= =" –" 1 .
=" –" 1 . ∴ OA^OB. …………… 3 分
(2) 设直线与x轴交于E, 则 E ( – 1 , 0 ) ∴|OE| =" 1" ,
S△OAB =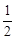 |OE|(| y 1| + | y 2| ) =
|OE|(| y 1| + | y 2| ) =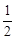 | y 1 – y 2| =
| y 1 – y 2| =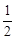
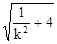 =
=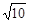 , 解得k = ±
, 解得k = ±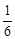 略
略
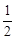 |OE|(| y 1| + | y 2| ) =
|OE|(| y 1| + | y 2| ) =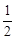 | y 1 – y 2| =
| y 1 – y 2| =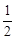
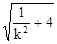 =
=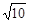 , 解得k = ±
, 解得k = ±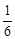 略
略
练习册系列答案
相关题目
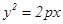 (
( )的焦点为
)的焦点为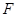 ,
, 为坐标原点,
为坐标原点,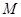 为抛物线上一点,且
为抛物线上一点,且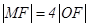 ,
,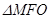 的面积为
的面积为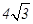 ,则该抛物线的方程为 .
,则该抛物线的方程为 . 直线
直线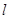 过抛物线的焦点
过抛物线的焦点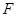 且与该抛物线交于
且与该抛物线交于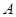 、
、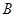 两点(点A在第一象限)
两点(点A在第一象限)  ,求直线
,求直线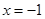 交于点
交于点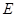 ,求证:
,求证: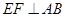 。
。 与圆
与圆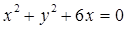 的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.  共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线方程.
,求双曲线方程. 的焦点为F,点A在y轴上,若线段FA的中点B在拋物线上,且点B到拋物线准线的距离为
的焦点为F,点A在y轴上,若线段FA的中点B在拋物线上,且点B到拋物线准线的距离为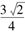 ,则点A的坐标为
,则点A的坐标为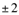 )
)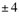 )
)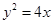 ,弦
,弦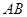 的中点
的中点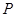 到
到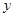 轴的距离为2,则弦
轴的距离为2,则弦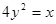 的焦点坐标是 .
的焦点坐标是 .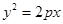 的焦点与椭圆
的焦点与椭圆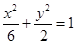 的左焦点重合,则
的左焦点重合,则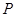 的值为( )
的值为( )