题目内容
将函数f(x)=sin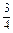 x·sin
x·sin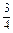 (x+2
(x+2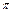 )·sin
)·sin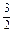 (x+3
(x+3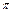 )在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an} (n=1,2,3,…).
)在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an} (n=1,2,3,…).
(1)求数列{an}的通项公式;
(2)设bn=sinansinan+1sinan+2,求证:bn=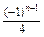 (n=1,2,3,…).
(n=1,2,3,…).
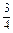 x·sin
x·sin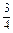 (x+2
(x+2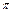 )·sin
)·sin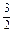 (x+3
(x+3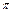 )在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an} (n=1,2,3,…).
)在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an} (n=1,2,3,…).(1)求数列{an}的通项公式;
(2)设bn=sinansinan+1sinan+2,求证:bn=
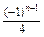 (n=1,2,3,…).
(n=1,2,3,…).(1)an=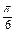 +(n-1)·
+(n-1)·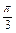 =
=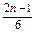
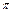 ,(n=1,2,3,…)(2)证明见解析
,(n=1,2,3,…)(2)证明见解析
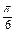 +(n-1)·
+(n-1)·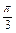 =
=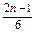
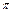 ,(n=1,2,3,…)(2)证明见解析
,(n=1,2,3,…)(2)证明见解析(1)解 ∵f(x)=sin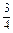 x·sin(
x·sin(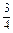 x+
x+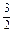
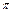 )·sin(
)·sin(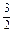 x+
x+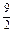
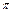 )
)
=sin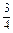 x·
x·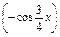 ·cos
·cos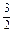 x
x
=-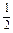 sin
sin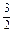 x·cos
x·cos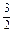 x=-
x=-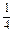 sin3x
sin3x
∴f(x)的极值点为x=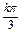 +
+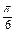 ,k∈Z,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以
,k∈Z,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以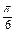 为首项,
为首项,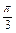 为公差的等差数列,
为公差的等差数列,
∴an=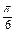 +(n-1)·
+(n-1)·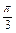 =
=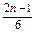
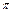 ,(n=1,2,3,…).
,(n=1,2,3,…).
(2)证明 由an=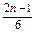
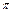 知对任意正整数n,an都不是
知对任意正整数n,an都不是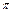 的整数倍.
的整数倍.
所以sinan≠0,从而bn=sinansinan+1sinan+2≠0.
于是 =
=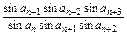 =
=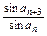
=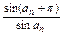 =-1.
=-1.
又b1=sin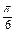 ·sin
·sin ·sin
·sin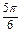 =
=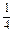 ,
,
{bn}是以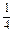 为首项,-1为公比的等比数列.
为首项,-1为公比的等比数列.
∴bn=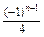 (n=1,2,3,…).
(n=1,2,3,…).
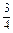 x·sin(
x·sin(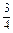 x+
x+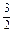
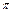 )·sin(
)·sin(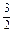 x+
x+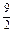
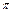 )
)=sin
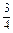 x·
x·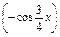 ·cos
·cos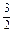 x
x=-
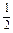 sin
sin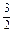 x·cos
x·cos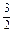 x=-
x=-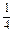 sin3x
sin3x∴f(x)的极值点为x=
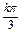 +
+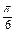 ,k∈Z,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以
,k∈Z,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以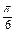 为首项,
为首项,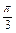 为公差的等差数列,
为公差的等差数列,∴an=
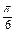 +(n-1)·
+(n-1)·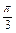 =
=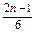
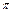 ,(n=1,2,3,…).
,(n=1,2,3,…).(2)证明 由an=
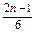
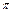 知对任意正整数n,an都不是
知对任意正整数n,an都不是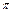 的整数倍.
的整数倍.所以sinan≠0,从而bn=sinansinan+1sinan+2≠0.
于是
 =
=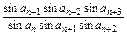 =
=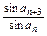
=
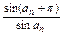 =-1.
=-1.又b1=sin
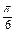 ·sin
·sin ·sin
·sin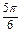 =
=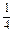 ,
,{bn}是以
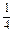 为首项,-1为公比的等比数列.
为首项,-1为公比的等比数列.∴bn=
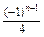 (n=1,2,3,…).
(n=1,2,3,…).
练习册系列答案
相关题目
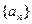 满足:
满足: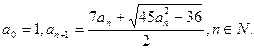
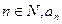 为正整数;(2)对任意
为正整数;(2)对任意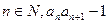 为完全平方数。
为完全平方数。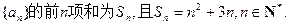
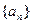 的通项公式; (II)求数列
的通项公式; (II)求数列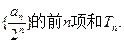
 , ak
, ak ,…, ak
,…, ak ,…成等比数列.
,…成等比数列. 的前n项和Sn.
的前n项和Sn.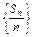 的前n项和,求Tn.
的前n项和,求Tn.