题目内容
设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列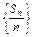 的前n项和,求Tn.
的前n项和,求Tn.
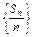 的前n项和,求Tn.
的前n项和,求Tn.Tn=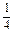 n2-
n2-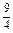 n
n
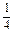 n2-
n2-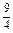 n
n 设等差数列{an}的公差为d,
则Sn=na1+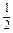 n(n-1)d,
n(n-1)d,
∵S7=7,S15=75,
∴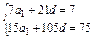 ,
,
即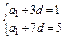 ,解得
,解得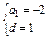 ,
,
∴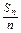 =a1+
=a1+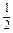 (n-1)d=-2+
(n-1)d=-2+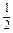 (n-1),
(n-1),
∵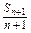 -
-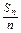 =
=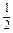 ,
,
∴数列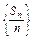 是等差数列,其首项为-2,公差为
是等差数列,其首项为-2,公差为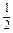 ,
,
∴Tn=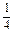 n2-
n2-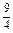 n.
n.
则Sn=na1+
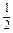 n(n-1)d,
n(n-1)d,∵S7=7,S15=75,
∴
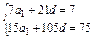 ,
,即
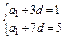 ,解得
,解得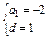 ,
,∴
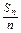 =a1+
=a1+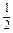 (n-1)d=-2+
(n-1)d=-2+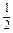 (n-1),
(n-1),∵
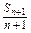 -
-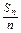 =
=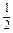 ,
,∴数列
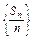 是等差数列,其首项为-2,公差为
是等差数列,其首项为-2,公差为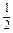 ,
,∴Tn=
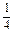 n2-
n2-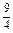 n.
n.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
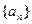 是以
是以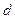 为公差的等差数列,数列
为公差的等差数列,数列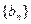 是以
是以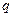 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列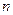 项和为
项和为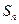 ,且
,且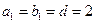 ,
,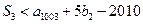 ,求整数
,求整数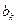 ,使得
,使得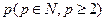 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若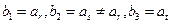 (其中
(其中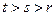 ,且(
,且(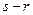 )是(
)是(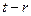 )的约数),求证:数列
)的约数),求证:数列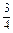 x·sin
x·sin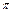 )·sin
)·sin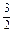 (x+3
(x+3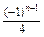 (n=1,2,3,…).
(n=1,2,3,…).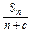 ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.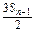 总成等差数列.
总成等差数列.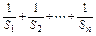 .
.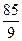 ,求这5个数.
,求这5个数.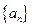 中,设
中,设 .
.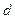 为公差的等差数列,求证
为公差的等差数列,求证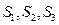 也是等差数列,并求其公差;
也是等差数列,并求其公差;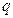 为公比的等比数列,求证
为公比的等比数列,求证