题目内容
已知等差数列{an}的公差为1,且a1+a2+a3+…+a99=99,则a3+a6+a9+…+a99的值是__________.
66
由已知a1+a2+a3+…+a99=99,
有99a1+(1+2+…+98)=99,
99a1+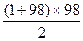
-99=0,∴99(a1+48)=0.
∴a1=-48,d=1.
∴a3+a6+a9+…+a99=a3+(a3+3)+(a3+6)+ …+［a3+(33-1)×3］
=33a3+3(1+2+3+…+32)=33a3+3×
=33×(-46+48)=66.
有99a1+(1+2+…+98)=99,
99a1+
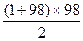-99=0,∴99(a1+48)=0.∴a1=-48,d=1.
∴a3+a6+a9+…+a99=a3+(a3+3)+(a3+6)+ …+［a3+(33-1)×3］
=33a3+3(1+2+3+…+32)=33a3+3×
=33×(-46+48)=66.
练习册系列答案
相关题目
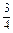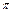x·sin
)·sin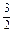
(x+3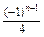
（n=1，2，3，…）.
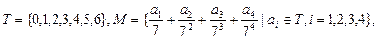将M中的元素按从大到小的顺序排列，则第2005个数是（ ）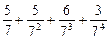
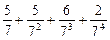
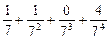
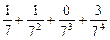
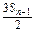总成等差数列.
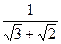，b=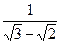
，则a、b的等差中项为（ ）
