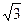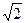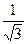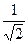题目内容
数列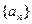 满足:
满足: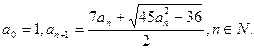
证明:(1)对任意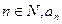 为正整数;(2)对任意
为正整数;(2)对任意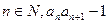 为完全平方数。
为完全平方数。
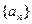 满足:
满足: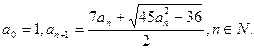
证明:(1)对任意
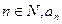 为正整数;(2)对任意
为正整数;(2)对任意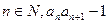 为完全平方数。
为完全平方数。 证明见解析
证明见解析证明:(1)由题设得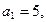 且
且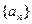 严格单调递增.将条件式变形得
严格单调递增.将条件式变形得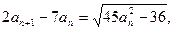 两边平方整理得
两边平方整理得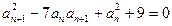 ①
①
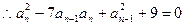 ②
②
①-②得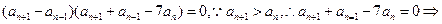
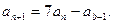 ③
③
由③式及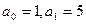 可知,对任意
可知,对任意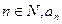 为正整数.…………………………10分
为正整数.…………………………10分
(2)将①两边配方,得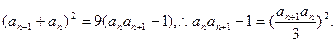 ④
④
由③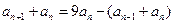 ≡
≡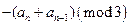
∴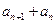 ≡
≡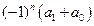 ≡0(mod3)∴
≡0(mod3)∴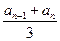 为正整数
为正整数
④式成立. 是完全平方数.……………………………………20分
是完全平方数.……………………………………20分
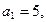 且
且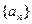 严格单调递增.将条件式变形得
严格单调递增.将条件式变形得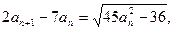 两边平方整理得
两边平方整理得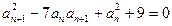 ①
①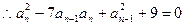 ②
②①-②得
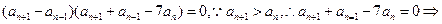
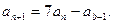 ③
③由③式及
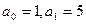 可知,对任意
可知,对任意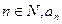 为正整数.…………………………10分
为正整数.…………………………10分(2)将①两边配方,得
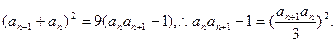 ④
④由③
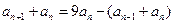 ≡
≡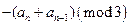
∴
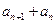 ≡
≡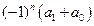 ≡0(mod3)∴
≡0(mod3)∴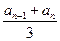 为正整数
为正整数④式成立.
 是完全平方数.……………………………………20分
是完全平方数.……………………………………20分
练习册系列答案
相关题目
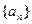 是以
是以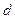 为公差的等差数列,数列
为公差的等差数列,数列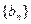 是以
是以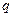 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列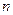 项和为
项和为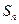 ,且
,且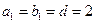 ,
,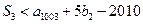 ,求整数
,求整数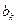 ,使得
,使得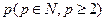 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若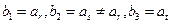 (其中
(其中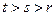 ,且(
,且(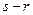 )是(
)是(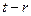 )的约数),求证:数列
)的约数),求证:数列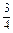 x·sin
x·sin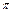 )·sin
)·sin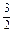 (x+3
(x+3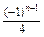 (n=1,2,3,…).
(n=1,2,3,…).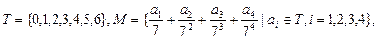 将M中的元素按从大到小的顺序排列,则第2005个数是( )
将M中的元素按从大到小的顺序排列,则第2005个数是( )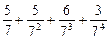
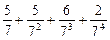
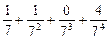
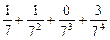
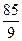 ,求这5个数.
,求这5个数.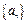
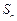
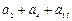
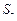
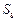
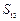
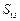
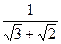 ,b=
,b=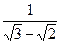 ,则a、b的等差中项为( )
,则a、b的等差中项为( )