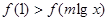题目内容
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) =" m" f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的函数.设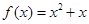 ,
,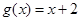 ,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且
,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且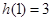 ,则函数h (x)="__________."
,则函数h (x)="__________."
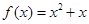 ,
,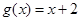 ,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且
,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且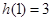 ,则函数h (x)="__________."
,则函数h (x)="__________." 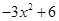
试题分析:依题意h(x)="m" f(x)+ng(x)=m(x2+x)+n(x+2)=mx2+mx+nx+2n
又h (x)为偶函数
则有h(x)=h(-x),即mx2+mx+nx+2n=mx2-mx-nx+2n
得出m+n=0
又h(1)=m+m+n+2n=3,即2m+3n=3
则有m+n=0,2m+3n=3,解得m=-3,n=3
所以h(x)=mx2+mx+nx+2n=-3x2-3x+3x+6=-3x2+6
故答案为:-3x2+6
点评:本题主要考查函数的奇偶性的运用.解题的关键是求出解析式中m和n的值

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
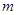 是实数,
是实数,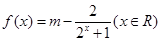 ,
,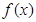 为奇函数,求
为奇函数,求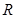 上为单调递增函数;
上为单调递增函数;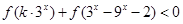 对任意
对任意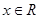 恒成立,求实数
恒成立,求实数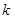 的取值范围。
的取值范围。 ,则
,则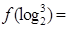 ( )
( )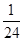
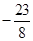
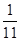
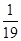
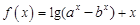 中,常数
中,常数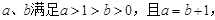 那么
那么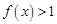 的解集为
的解集为
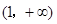
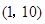
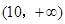
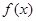 与函数
与函数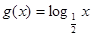 的图像关于直线
的图像关于直线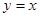 对称,则函数
对称,则函数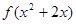 的单调递增区间是
的单调递增区间是 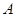 和
和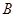 的含铁率
的含铁率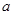 ,冶炼每万吨铁矿石的
,冶炼每万吨铁矿石的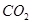 的排放量
的排放量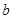 及每万吨铁矿石的价格
及每万吨铁矿石的价格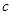 如下表:
如下表: (万吨),则购买铁矿石的最少费用为
(万吨),则购买铁矿石的最少费用为 (百万元).
(百万元).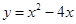 ,其中
,其中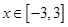 ,则该函数的值域为___________.
,则该函数的值域为___________.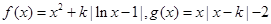 ,其中
,其中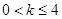 .(1) 讨论函数
.(1) 讨论函数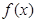 的单调性,并求出
的单调性,并求出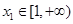 ,都存在
,都存在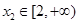 ,使得
,使得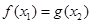 ,求实数
,求实数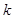 的取值范围.
的取值范围.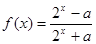 ,若
,若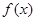 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数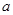 的值;(2)求函数
的值;(2)求函数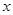 的不等式:
的不等式: