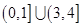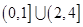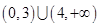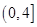题目内容
(本小题满分16分)
已知函数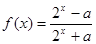 ,若
,若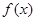 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数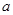 的值;(2)求函数
的值;(2)求函数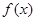 的值域;(3)求证:
的值域;(3)求证: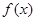 在R上为增函数;(4)若m为实数,解关于
在R上为增函数;(4)若m为实数,解关于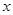 的不等式:
的不等式: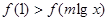
已知函数
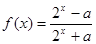 ,若
,若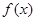 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数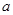 的值;(2)求函数
的值;(2)求函数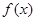 的值域;(3)求证:
的值域;(3)求证: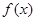 在R上为增函数;(4)若m为实数,解关于
在R上为增函数;(4)若m为实数,解关于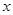 的不等式:
的不等式: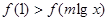
(1)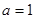 ;(2)
;(2)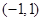 ; (3)设
; (3)设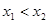 ,则
,则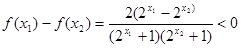 ,所以
,所以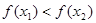 ,
,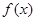 在R上为增函数。 (4)当m>0时,
在R上为增函数。 (4)当m>0时,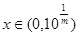 ;当
;当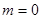 时,
时,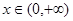 ;当
;当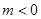 时,
时,
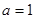 ;(2)
;(2)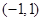 ; (3)设
; (3)设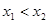 ,则
,则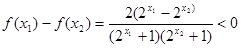 ,所以
,所以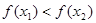 ,
,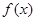 在R上为增函数。 (4)当m>0时,
在R上为增函数。 (4)当m>0时,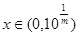 ;当
;当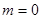 时,
时,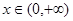 ;当
;当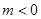 时,
时,
试题分析:(1)由f(0)=0得
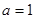 (3分)
(3分)(2)
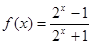 ,则
,则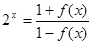 ,由
,由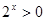 ,得
,得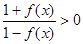
解得
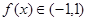 (6分)
(6分)(3)设
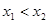 ,则
,则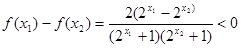 ,
,所以
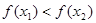 ,
,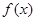 在R上为增函数。(9分)
在R上为增函数。(9分)(4)因为
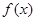 在R上为增函数,所以
在R上为增函数,所以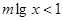 ,(10分)
,(10分)当m>0时,
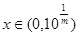 ;(12分) 当
;(12分) 当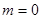 时,
时,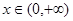 ;(14分) 当
;(14分) 当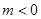 时,
时, (16分)
(16分)点评:函数的单调性主要考查:⑴会用定义证明(或判断)函数在已知区间上的单调性;⑵会求已知函数(包括简单的复合函数)的单调区间;⑶能利用函数的单调性比较两个数的大小或求变量的取值范围;⑷能利用函数的单调性求已知函数在给定区间上的最大值或最小值。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
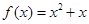 ,
,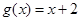 ,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且
,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且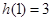 ,则函数h (x)="__________."
,则函数h (x)="__________." 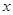 天(
天(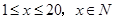 )的销售价格(单位:元)为
)的销售价格(单位:元)为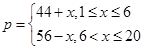 ,第
,第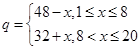 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.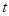 关于第
关于第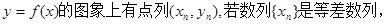 数列{
数列{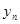 }是等比数列,则函数
}是等比数列,则函数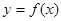 的解析式可能为( )
的解析式可能为( )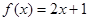
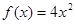
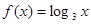
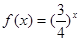
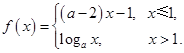 若
若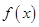 在
在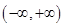 上单调递增,则实数
上单调递增,则实数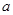 的取值范围为( )
的取值范围为( )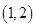
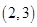
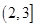
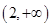
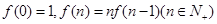 ,则
,则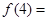
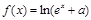 (
(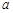 为常数)是实数集
为常数)是实数集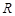 上的奇函数,函数
上的奇函数,函数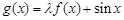 是区间
是区间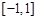 上的减函数。
上的减函数。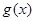 在
在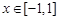 上的最大值;
上的最大值;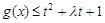 对
对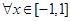 及
及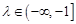 恒成立,求
恒成立,求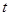 的取值范围;
的取值范围;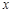 的方程
的方程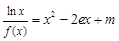 的根的个数。
的根的个数。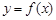 满足:①
满足:①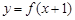 是偶函数;②在区间
是偶函数;②在区间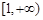 上是增函数.若
上是增函数.若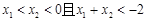 ,则
,则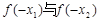 的大小关系是( )
的大小关系是( )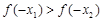
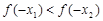
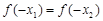
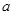 和
和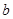 ,定义运算“
,定义运算“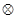 ”:
”: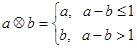 ,设函数
,设函数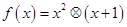 ,若函数
,若函数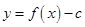 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数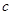 的取值范围是 ( )
的取值范围是 ( )