题目内容
13．已知函数f（x）=x2+|x+1-a|，其中a为实常数，在x（-$\frac{1}{2}$，$\frac{1}{2}$）单调递增，求a的范围．分析 分类得出（1）当x≥a-1时，函数f（x）=（x+$\frac{1}{2}$）2$+\frac{3}{4}$-a，其中a为实常数，利用单调性得出a-1$≤-\frac{1}{2}$，求解即可
（2）当x＜a-1时，函数f（x）=x2-x-1+a，其中a为实常数，f（x）=（x$-\frac{1}{2}$）2$-\frac{3}{4}$+a，判断在x（-$\frac{1}{2}$，$\frac{1}{2}$）单调递增，不符合题意，总结可得出答案．
解答 解：（1）当x≥a-1时，函数f（x）=x2+|x+1-a|，其中a为实常数，
f（x）=（x+$\frac{1}{2}$）2$+\frac{3}{4}$-a，
∵在x（-$\frac{1}{2}$，$\frac{1}{2}$）单调递增，
∴a-1$≤-\frac{1}{2}$，即a$≤\frac{1}{2}$，
（2）当x＜a-1时，函数f（x）=x2-x-1+a，其中a为实常数，
f（x）=（x$-\frac{1}{2}$）2$-\frac{3}{4}$+a，
∴在x（-$\frac{1}{2}$，$\frac{1}{2}$）单调递减函数，
即可得出：不符合题意．
综上：a$≤\frac{1}{2}$
点评 本题考查了分类思想的运用，二次函数的性质，不等式的运用，属于中档题．
练习册系列答案
相关题目
4．已知两个集合A={x|y=ln（-x2+x+2）}，$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=（ ）
| A． | $[{-\frac{1}{2}，2}）$ | B． | $（{-1，-\frac{1}{2}}]$ | C． | （-1，e） | D． | （2，e） |
18．
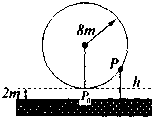一个大风车的半径为8m，12min旋转一周，它的最低点P0离地面2m，风车翼片的一个端点P从P0开始按逆时针方向旋转，则点P离地面距离h（m）与时间f（min）之间的函数关系式是（ ）
一个大风车的半径为8m，12min旋转一周，它的最低点P0离地面2m，风车翼片的一个端点P从P0开始按逆时针方向旋转，则点P离地面距离h（m）与时间f（min）之间的函数关系式是（ ）| A． | h（t）=-8sin$\frac{π}{6}$t+10 | B． | h（t）=-cos$\frac{π}{6}$t+10 | C． | h（t）=-8sin$\frac{π}{6}$t+8 | D． | h（t）=-8cos$\frac{π}{6}$t+10 |
