题目内容
4.已知两个集合A={x|y=ln(-x2+x+2)},$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=( )| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |
分析 求出A中x的范围确定出A,求出B中不等式的解集确定出B,找出A与B的交集即可.
解答 解:由A中y=ln(-x2+x+2),得到-x2+x+2>0,即(x-2)(x+1)<0,
解得:-1<x<2,即A=(-1,2),
由B中不等式变形得:$\frac{2e+1}{e-x}$-2≤0,即$\frac{2x+1}{e-x}$≤0,
整理得:(2x+1)(x-e)≥0,且x-e≠0,
解得:x≤-$\frac{1}{2}$或x>e,即B=(-∞,-$\frac{1}{2}$]∪(e,+∞),
则A∩B=(-1,-$\frac{1}{2}$].
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
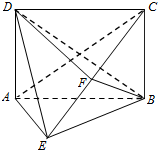 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,