题目内容
3.解答下列问题:(1)设α为第三象限角,求$\frac{|sinα|}{sinα}$-$\frac{2cosα}{|cosα|}$的值;
(2)已知tan(-α)=2,求$\frac{sin(α-720°)+cos(180°+α)}{sin(-α)-cos(-α)}$的值.
分析 (1)由α位置确定sinα,cosα的符号,化简求值;
(2)已知tan(-α)=2得到tanα,利用诱导公式化简三角函数式,然后求值.
解答 解:(1)因为α为第三象限角,所以sinα<0,cosα<0,所以$\frac{|sinα|}{sinα}$-$\frac{2cosα}{|cosα|}$=$\frac{-sinα}{sinα}-\frac{2cosα}{-cosα}$=-1+2=1;
(2)由tan(-α)=2,得到tanα=-2,
又$\frac{sin(α-720°)+cos(180°+α)}{sin(-α)-cos(-α)}$=$\frac{sinα-cosα}{-sinα-cosα}$=$\frac{tanα-1}{-tanα-1}=\frac{-2-1}{2-1}$=-3.
点评 本题考查了三角函数各象限的符号以及诱导公式的运用;注意三角函数名称以及符号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.复数$\frac{3+2i}{1-i}$=( )
| A. | $\frac{1}{2}+\frac{5}{2}i$ | B. | $\frac{1}{2}-\frac{5}{2}i$ | C. | $-\frac{1}{2}+\frac{5}{2}i$ | D. | $-\frac{1}{2}-\frac{5}{2}i$ |
18.已知复数z=1+i+i2+…i10,则复数z在复平面内对应的点为( )
| A. | (1,1) | B. | (1,-1) | C. | (0,1) | D. | (1,0) |
15.点P在直径为5的球面上,过P作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| A. | 2$\sqrt{14}$ | B. | 2$\sqrt{70}$ | C. | $\sqrt{70}$ | D. | $\sqrt{14}$ |
12.如图所示的程序框图运行结束后,输出的集合中包含的元素个数为( )
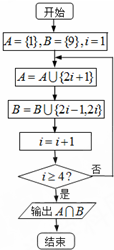

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.
如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.