题目内容
2.已知函数f(x)=sin(ωx+φ)+1(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的最小正周期为π,图象过点P(0,1)(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设函数 g(x)=f(x)+cos2x-1,将函数 g(x)图象上所有的点向右平行移动$\frac{π}{4}$个单位长度后,所得的图象在区间(0,m)内是单调函数,求实数m的最大值.
分析 (Ⅰ)由已知中函数f(x)的最小正周期为π,图象过点P(0,1),求出ω,φ的值,可得函数f(x)的解析式;
(Ⅱ)求出函数 g(x)=f(x)+cos2x-1的解析式及将函数 g(x)图象上所有的点向右平行移动$\frac{π}{4}$个单位长度后的解析式,结合正弦函数的图象和性质及所得的图象在区间(0,m)内是单调函数,可得m的范围.
解答 解:(Ⅰ)∵函数f(x)=sin(ωx+φ)+1(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的最小正周期为π,
∴ω=$\frac{2π}{π}$=2,
又由函数f(x)的图象过点P(0,1),
∴sinφ=0,
∴φ=0,
∴函数f(x)=sin2x+1;
(Ⅱ)∵函数 g(x)=f(x)+cos2x-1=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
将函数 g(x)图象上所有的点向右平行移动$\frac{π}{4}$个单位长度后,
所得函数的解析式是:h(x)=$\sqrt{2}$sin[2(x-$\frac{π}{4}$)+$\frac{π}{4}$]=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
∵x∈(0,m),
∴2x-$\frac{π}{4}$∈(-$\frac{π}{4}$,2m-$\frac{π}{4}$),
又由h(x)在区间(0,m)内是单调函数,
∴2m-$\frac{π}{4}$≤$\frac{π}{2}$,即m≤$\frac{3π}{8}$,
即实数m的最大值为$\frac{3π}{8}$.
点评 本题考查的知识点是正弦型函数的图象和性质,函数图象的平移变换,熟练掌握正弦型函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
17.对于定义在R上的函数f(x),若存在x0使得$\underset{\underbrace{f(f…(f({x}_{0})))}}{k}$=x0(*),其中k为某个正整数,则称x0为函数f(x)的一个周期点,使得(*)式成立的正整数k称为x0的周期,使得(*)式成立的最小正整数k称为x0的最小周期,若函数f(x)=1-|2x-1|,则函数f(x)( )
| A. | 恰有一个最小周期为1的周期点,恰有一个最小周期为2的周期点 | |
| B. | 恰有一个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| C. | 恰有两个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| D. | 恰有两个最小周期为1的周期点,恰有四个最小周期为2的周期点 |
7.若执行如图所示的程序框图,则输出的i的值为( )
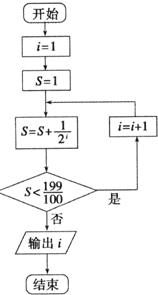

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
11.复数$\frac{3+2i}{1-i}$=( )
| A. | $\frac{1}{2}+\frac{5}{2}i$ | B. | $\frac{1}{2}-\frac{5}{2}i$ | C. | $-\frac{1}{2}+\frac{5}{2}i$ | D. | $-\frac{1}{2}-\frac{5}{2}i$ |
12.如图所示的程序框图运行结束后,输出的集合中包含的元素个数为( )
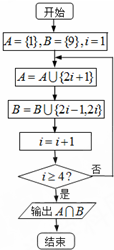

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
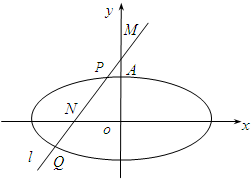 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.