题目内容
【题目】如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,AB⊥AD,AB=3,CD=2,PD=AD=5. 
(1)在PD上确定一点E,使得PB∥平面ACE,并求 ![]() 的值;
的值;
(2)在(1)条件下,求平面PAB与平面ACE所成锐二面角的余弦值.
【答案】
(1)解:连接BD交AC于O,
在△PBD中,过O作OE∥BP交PD于E,
∵OE平面ACE,PB平面ACE,
∴PB∥平面ACE,
∵AB=3,CD=2,∴ ![]()
(2)解:以D为坐标原点,建立如图所示的空间直角坐标系,
则A(5,0,0),C(0,2,0),D(0,0,0),E(0,0,2),P(0,0,5),
![]() =(5,﹣2,0),
=(5,﹣2,0), ![]() =(0,﹣2,2),
=(0,﹣2,2),
设平面ACE的一个法向量为n=(x,y,z),
则 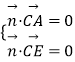 ,即
,即 ![]() ,
,
令z=5,则x=2,y=5,∴n=(2,5,5)
取PA的中点为F,连接DF,∵AD=PD,∴DF⊥PA,
又AB⊥平面PAD,∴AB⊥DF,则DF⊥平面PAB,
即 ![]() =(
=( ![]() ,0,
,0, ![]() )是平面PAB的一个法向量,
)是平面PAB的一个法向量,
∴cos< ![]() >=
>= ![]() =
= 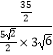 =
= ![]() ,
,
∴平面PAB与平面ACE所成锐二面角的余弦值为 ![]() .
.

【解析】(1)连接BD交AC于O,过O作OE∥BP交PD于E,推导出PB∥平面ACE,由此能求出 ![]() 的值.(2)以D为坐标原点,建立空间直角坐标系,利用向量法能求出平面PAB与平面ACE所成锐二面角的余弦值.
的值.(2)以D为坐标原点,建立空间直角坐标系,利用向量法能求出平面PAB与平面ACE所成锐二面角的余弦值.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(m) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?




