题目内容
【题目】已知曲线C： 
=1（y≥0），直线l：y=kx+1与曲线C交于A，D两点，A，D两点在x轴上的射影分别为点B，C．记△OAD的面积S1 ， 四边形ABCD的面积为S2 ． （Ⅰ）当点B坐标为（﹣1，0）时，求k的值；
（Ⅱ）若S1= 
，求线段AD的长；
（Ⅲ）求 
的范围．
【答案】解：（Ⅰ）由题意，y=kx+1与曲线C交于A，D两点，A，D两点在x轴上的射影分别为点B，C．点B坐标为（﹣1，0）， 则点A的横坐标为﹣1，代入曲线C： 
=1（y≥0），解得点A的纵坐标为x= 
，
即A（﹣1， ）
∵点A在直线y=kx+1，则有： =k×（﹣1）+1，
∴解得k=﹣ 
，
k的值﹣ ；
（Ⅱ）由题意，k不存在时，四边形ABCD也不存在，则k必须存在．
设点A（xA ， yA），点D（xD ， yD），则点B（xA ， 0），点C（xD ， 0）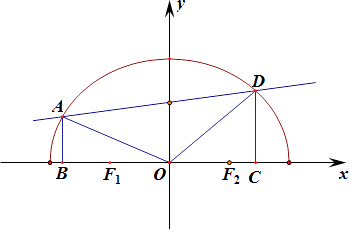
直线l：y=kx+1与曲线C交于A，D两点，
A，D两点代入曲线C，即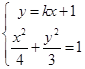 
，消去y，整理得：（3+4k2）x2+8kx﹣8=0，
由直线l经过椭圆左右顶点时，k=± ，
则﹣ ≤k≤ ，
解得：xA+xD=﹣ 
，xAxD= 
，|AD|= 
= 
，
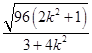△OAD的面积为S1 ， 设原点（0，0）到直线l：y=kx+1距离为h，
则h= 
，
S1= 
= |AD|h= 
= ，整理得：40k4+11k2﹣2=0，则k2= 
，
解得k=± 
，|AD|= 
，
∴线段AD的长 
；
（Ⅲ）由题意及（i）：可知：S2= （y1+y2）丨x1﹣x2丨，
则 
= 
= 
，
由y1+y2=kx1+1+kx2+1=k（x1+x2）+2，
∴ = = 
= 
，
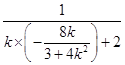由﹣ ≤k≤ ，
∴ ≤ ≤ 
，
∴ 的取值范围[ ， ]．
【解析】（Ⅰ）由题意B（﹣1，0），将x=﹣1代入椭圆方程，即可求得A点坐标，代入直线方程，即可求得k的值；（Ⅱ）将直线方程代入椭圆方程，由题意求得k的取值范围，利用韦达定理及弦长公式求得丨AD丨，根据三角形的面积公式，即可求得k的值，求得丨AD丨，（Ⅲ）求得，四边形ABCD的面积为S2 ， 求得 
的表达式，由k的取值范围，即可求得 的取值范围．
