题目内容
【题目】已知幂函数f(x)＝mxα的图象经过点A(2,2).
(1)试比较2ln f(3)与3ln f(2)的大小；
(2)定义在R上的函数g(x)满足g(-x)=g(x), g(4+x)=g(4-x)，且当x∈[0,4]时，
. 若关于x的不等式g 2(x)+ng(x)>0在[-200,200]上有且只有151个整数解，求实数n的取值范围。
【答案】(1) 2ln f(3)>3ln f(2)..
(2) 
.
【解析】分析：（1）两数相除与1比较大小即可；
（2）由(
)′＝
知,函数y＝在[1,e]单调递增,在(e,4]单调递减，
g(-x)=g(x)且g(4+x)=g(4-x)，故g(4+x)=g(x-4)，从而g(x)为周期T=8的偶函数.画出g(x)在一个周期内的图象，利用数形结合分析即可.
详解：函数f(x)＝mxα为幂函数，所以m＝1；又由于其图象经过点A(2,2)，则有α＝1.所以f(x)＝x.
(1)
＝
＝
＝
>1
由于2ln f(3)>0, 3ln f(2)>0, 所以2ln f(3)>3ln f(2).
(2) 由()′＝知,函数y＝在[1,e]单调递增,在(e,4]单调递减.
因为g(-x)=g(x)且g(4+x)=g(4-x),故g(4+x)=g(x-4),从而g(x)为周期T=8的偶函数.
由当x∈[0,4]时，g(x)＝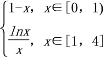
, 得g(x)在一个周期内的图像如图所示:
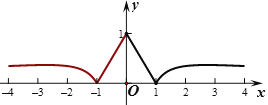
①当n=0时，显然不合题意;
②当n>0时，g 2(x)+ng(x)>0g(x)[g(x)+n]>0g(x)<-n或g(x)>0.
在[-200,200]上的整数解共有401-100=301个，显然不合题意；
③当n<0时，g2(x)+ng(x)>0g(x)[g(x)+n]>0g(x)<0或g(x)>-n.
由(1)知: 
>
=
, 要使不等式g 2(x)+ng(x)>0在[-200,200]上有且只有151个整数解, 只需≤-n<, 解得:- <n≤-.
综上, -<n≤-.
