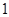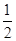题目内容
已知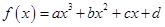 是定义在R上的函数,其图象交
是定义在R上的函数,其图象交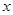 轴于A、B、C三点,若B点坐标为
轴于A、B、C三点,若B点坐标为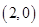 ,且
,且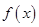 在
在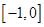 和
和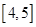 上有相同的单调性,在
上有相同的单调性,在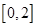 和
和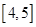 上有相反的单调性.
上有相反的单调性.
(1)求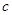 的值;
的值;
(2)在函数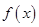 的图象上是否存在一点
的图象上是否存在一点 ,使得
,使得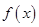 在点M的切线的斜率为
在点M的切线的斜率为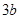 ?若存在,求出M点的坐标;若不存在,说明理由;
?若存在,求出M点的坐标;若不存在,说明理由;
(3)求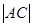 的取值范围.
的取值范围.
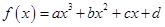 是定义在R上的函数,其图象交
是定义在R上的函数,其图象交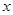 轴于A、B、C三点,若B点坐标为
轴于A、B、C三点,若B点坐标为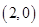 ,且
,且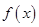 在
在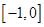 和
和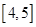 上有相同的单调性,在
上有相同的单调性,在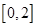 和
和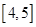 上有相反的单调性.
上有相反的单调性.(1)求
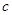 的值;
的值;(2)在函数
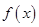 的图象上是否存在一点
的图象上是否存在一点 ,使得
,使得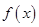 在点M的切线的斜率为
在点M的切线的斜率为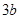 ?若存在,求出M点的坐标;若不存在,说明理由;
?若存在,求出M点的坐标;若不存在,说明理由;(3)求
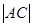 的取值范围.
的取值范围.(1)0;(2)不存在;(3)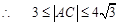
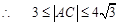
(1)根据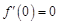 ,可求出c值。
,可求出c值。
(2)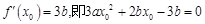 ,
,
然后研究其方程是否有根据即可。
(3)解题的关键是先表示出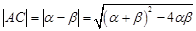
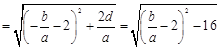 ,然后根据第(2)问求得的
,然后根据第(2)问求得的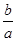 的范围转化为函数问题解决即可。
的范围转化为函数问题解决即可。
解:(1)因为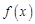 在
在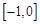 和
和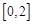 上有相反的单调性
上有相反的单调性
所以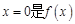 的一个极值点,故
的一个极值点,故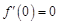
即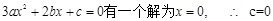 …………………………4分
…………………………4分
(2)因为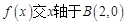
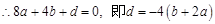
令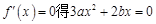
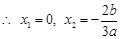
因为在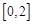 和
和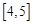 上有相反的单调性
上有相反的单调性
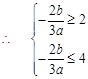
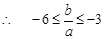 ………………………………………………………………6分
………………………………………………………………6分
假设存在点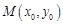 使得
使得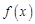 在点M的切线的斜率为
在点M的切线的斜率为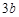
则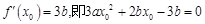
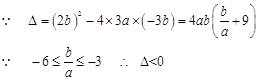
故不存在点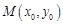 满足(2)中的条件。……………………………………9分
满足(2)中的条件。……………………………………9分
(3)设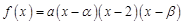
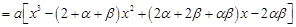
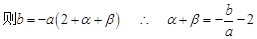
 ………………………………………10分
………………………………………10分
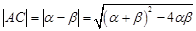
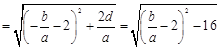 …………………………………………12分
…………………………………………12分
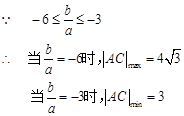
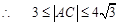 ……………………………………………………………14分
……………………………………………………………14分
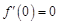 ,可求出c值。
,可求出c值。(2)
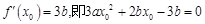 ,
,然后研究其方程是否有根据即可。
(3)解题的关键是先表示出
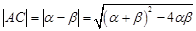
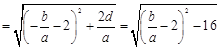 ,然后根据第(2)问求得的
,然后根据第(2)问求得的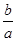 的范围转化为函数问题解决即可。
的范围转化为函数问题解决即可。解:(1)因为
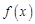 在
在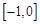 和
和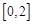 上有相反的单调性
上有相反的单调性所以
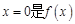 的一个极值点,故
的一个极值点,故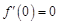
即
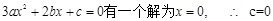 …………………………4分
…………………………4分(2)因为
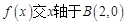
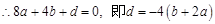
令
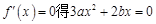
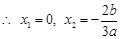
因为在
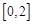 和
和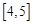 上有相反的单调性
上有相反的单调性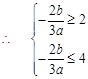
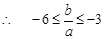 ………………………………………………………………6分
………………………………………………………………6分假设存在点
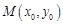 使得
使得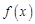 在点M的切线的斜率为
在点M的切线的斜率为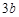
则
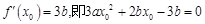
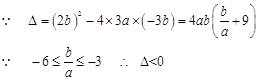
故不存在点
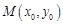 满足(2)中的条件。……………………………………9分
满足(2)中的条件。……………………………………9分(3)设
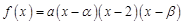
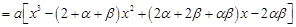
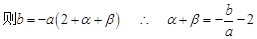
 ………………………………………10分
………………………………………10分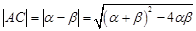
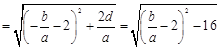 …………………………………………12分
…………………………………………12分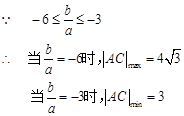
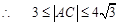 ……………………………………………………………14分
……………………………………………………………14分
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
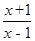 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间; 与
与 ,
,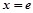 及
及 轴围成图形的面积是( )
轴围成图形的面积是( )

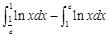

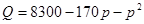 .问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。
.问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。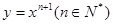 在点(1,1)处的切线与
在点(1,1)处的切线与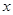 轴的交点的横坐标为
轴的交点的横坐标为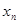 ,令
,令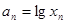 ,则
,则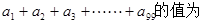 ______________
______________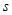 (米)与时间
(米)与时间 (秒)满足
(秒)满足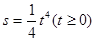 ,如果它在
,如果它在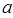 秒内的平均速度与
秒内的平均速度与 秒时的瞬时速度相等,则
秒时的瞬时速度相等,则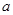 等于( )
等于( )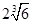
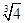
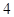
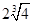
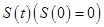 ,则导函数
,则导函数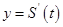 的图像大致 ( )
的图像大致 ( )
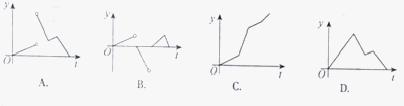
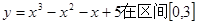 上的最大值和最小值分别是( ).
上的最大值和最小值分别是( ).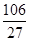
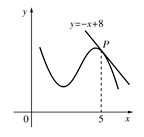
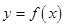 的图象在点P处的切线方程是
的图象在点P处的切线方程是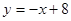 ,则
,则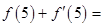 ( )
( )