题目内容
已知函数f (x)=lnx,g(x)=ex.
(I)若函数φ (x) = f (x)-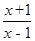 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(Ⅱ)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
(I)若函数φ (x) = f (x)-
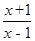 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;(Ⅱ)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
(1)增区间为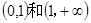 ;(2)见解析.
;(2)见解析.
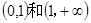 ;(2)见解析.
;(2)见解析.本试题主要是考查了导数在研究函数中的运用。
解:(Ⅰ)
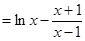 ,
,
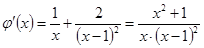 . 2分
. 2分
∵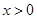 且
且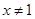 ,
,
∴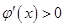
∴函数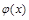 的单调递增区间为
的单调递增区间为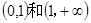 . 4分
. 4分
(Ⅱ)∵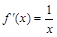 ,∴
,∴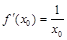 ,
,
∴ 切线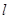 的方程为
的方程为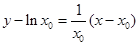 ,
,
即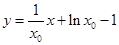 , ① 6分
, ① 6分
设直线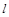 与曲线
与曲线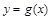 相切于点
相切于点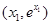 ,
,
∵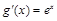 ,∴
,∴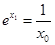 ,∴
,∴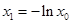 . 8分
. 8分
∴直线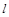 也为
也为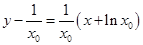 ,
,
即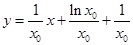 , ② 9分
, ② 9分
由①②得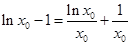 ,
,
∴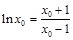 . 11分
. 11分
下证:在区间(1,+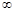 )上
)上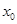 存在且唯一.
存在且唯一.
由(Ⅰ)可知,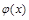
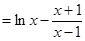 在区间
在区间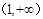 上递增.
上递增.
又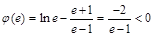 ,
,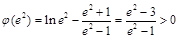 , 13分
, 13分
结合零点存在性定理,说明方程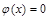 必在区间
必在区间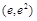 上有唯一的根,这个根就是所求的唯一
上有唯一的根,这个根就是所求的唯一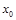 .
.
故结论成立. 14分
解:(Ⅰ)

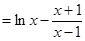 ,
,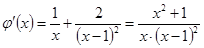 . 2分
. 2分∵
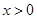 且
且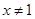 ,
,∴
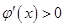
∴函数
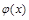 的单调递增区间为
的单调递增区间为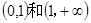 . 4分
. 4分(Ⅱ)∵
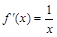 ,∴
,∴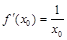 ,
,∴ 切线
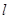 的方程为
的方程为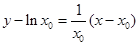 ,
,即
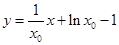 , ① 6分
, ① 6分设直线
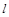 与曲线
与曲线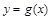 相切于点
相切于点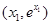 ,
,∵
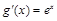 ,∴
,∴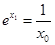 ,∴
,∴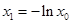 . 8分
. 8分∴直线
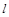 也为
也为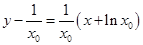 ,
, 即
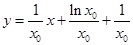 , ② 9分
, ② 9分由①②得
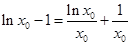 ,
,∴
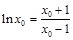 . 11分
. 11分下证:在区间(1,+
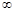 )上
)上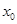 存在且唯一.
存在且唯一.由(Ⅰ)可知,
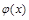
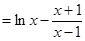 在区间
在区间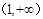 上递增.
上递增.又
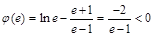 ,
,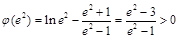 , 13分
, 13分结合零点存在性定理,说明方程
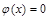 必在区间
必在区间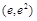 上有唯一的根,这个根就是所求的唯一
上有唯一的根,这个根就是所求的唯一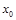 .
. 故结论成立. 14分

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
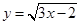 在点(1,
在点(1,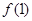 )处的切线方程为 ( )
)处的切线方程为 ( )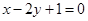
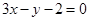
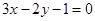
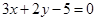
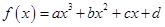 是定义在R上的函数,其图象交
是定义在R上的函数,其图象交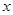 轴于A、B、C三点,若B点坐标为
轴于A、B、C三点,若B点坐标为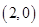 ,且
,且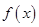 在
在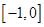 和
和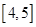 上有相同的单调性,在
上有相同的单调性,在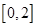 和
和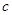 的值;
的值; ,使得
,使得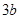 ?若存在,求出M点的坐标;若不存在,说明理由;
?若存在,求出M点的坐标;若不存在,说明理由;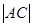 的取值范围.
的取值范围.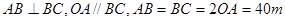 ,曲线段
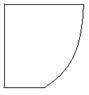
,曲线段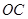 是以点
是以点 为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在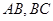 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段
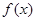 的导函数为
的导函数为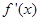 ,且满足
,且满足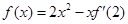 ,则
,则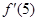 = .
= .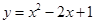 在点(1,0)处的切线方程为 * *
在点(1,0)处的切线方程为 * * 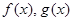 在
在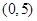 内的导数均存在,且有以下数据:
内的导数均存在,且有以下数据:
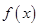
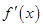
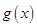
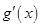
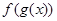 在
在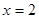 处的导数值是 .
处的导数值是 .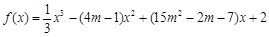 在
在 上是增函数,则
上是增函数,则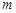 的取值范围为 .
的取值范围为 . ,若
,若 ,则
,则 的值等于
的值等于


