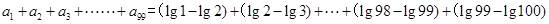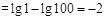题目内容
设函数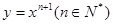
在点（1，1）处的切线与
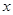轴的交点的横坐标为
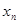，令
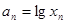，则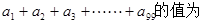
______________
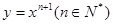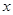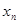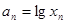在点（1，1）处的切线与轴的交点的横坐标为，令，则______________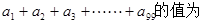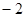
∵
，∴
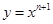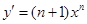，∴在点（1，1）处的切线斜率为n+1，∴切线方程为y=(n+1)x-n，∴切线与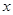轴的交点的横坐标为
，∴
，∴
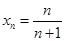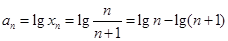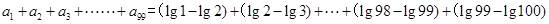
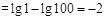
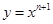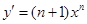，∴，∴在点（1，1）处的切线斜率为n+1，∴切线方程为y=(n+1)x-n，∴切线与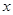轴的交点的横坐标为，∴，∴
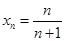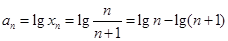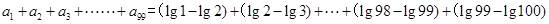
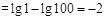
练习册系列答案
相关题目
题目内容
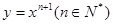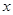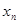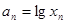在点（1，1）处的切线与轴的交点的横坐标为，令，则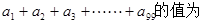______________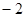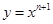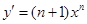，∴，∴在点（1，1）处的切线斜率为n+1，∴切线方程为y=(n+1)x-n，∴切线与轴的交点的横坐标为，∴，∴
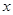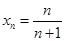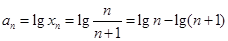看作时间
的函数，其图像可能是（ ）
是定义在R上的函数，其图象交
轴于A、B、C三点，若B点坐标为
，且
在
和
上有相同的单调性，在
和
的值；
，使得
？若存在，求出M点的坐标；若不存在，说明理由；
的取值范围．
，曲线
在点x=1处的切线为
，若
时，
的值； （2）求
上的最大值和最小值。
在点（1，1）处的切线与
轴的交点的横坐标为
,令
，则
的值为 .
的导数是（ ）
的导数为
的导数为
的导数为
。若
（用分数表示）
在点（1,0）处的切线方程为 ( ) 
