题目内容
已知曲线y=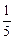
x5上一点M处的切线与直线y=3－x垂直,则此切线方程只能是
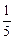x5上一点M处的切线与直线y=3－x垂直,则此切线方程只能是| A．5x＋5y－4="0" | B．5x－5y－4=0 |
| C．5x－5y＋4="0" | D．5x－5y±4=0 |
D
本题考查导数的几何意义及直线间的关系.两条都存在斜率的直线垂直,斜率乘积等于－1.
曲线过M点的切线的斜率为1.
由y′=x4,令y′=x4=1得x1=－1或x2=1.
把x1=－1和x2=1代入曲线中,得y1=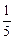－,y2=,
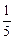即M1(－1,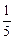－)或M2(1, ).
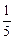所以过M点的切线方程为y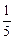＋=1·(x＋1)或y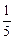－=1·(x－1),
即5x－5y＋4=0或5x－5y－4=0.
曲线过M点的切线的斜率为1.
由y′=x4,令y′=x4=1得x1=－1或x2=1.
把x1=－1和x2=1代入曲线中,得y1=－
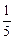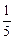,y2=,即M1(－1,－
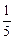)或M2(1, 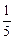).所以过M点的切线方程为y＋
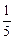=1·(x＋1)或y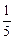－=1·(x－1),即5x－5y＋4=0或5x－5y－4=0.
练习册系列答案
相关题目
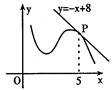
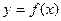的图象在点P处的切线方程是 
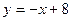，则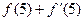
= .
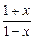,F(x)=
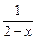+f(x). 
;
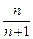x3＋x
的另一点A，问电灯与点0的距离怎样，可使点A处有最大的照度？（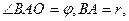
照度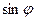与
成正比，与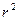
成反比）
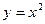到直线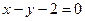
的最短距离为（ ）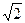
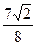
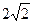
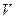的圆柱形水池，已知底的单位面积造价是侧面单位造价的一半，问：如何设计水池的底半径和高，才能使总造价最省？
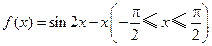的最值。