题目内容
设f(x)=log2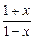 ,F(x)=
,F(x)=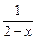 +f(x).
+f(x).
(1)试判断函数f(x)的单调性,并用函数单调性定义,给出证明;
(2)若f(x)的反函数为f-1(x),证明: 对任意的自然数n(n≥3),都有f-1(n)>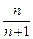 ;
;
(3)若F(x)的反函数F-1(x),证明: 方程F-1(x)=0有惟一解.
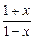 ,F(x)=
,F(x)=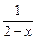 +f(x).
+f(x). (1)试判断函数f(x)的单调性,并用函数单调性定义,给出证明;
(2)若f(x)的反函数为f-1(x),证明: 对任意的自然数n(n≥3),都有f-1(n)>
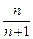 ;
;(3)若F(x)的反函数F-1(x),证明: 方程F-1(x)=0有惟一解.
(1) F(x)在(-1,1)上是增函数,(2)证明略 (3)证明略
(1)由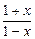 >0,且2-x≠0得F(x)的定义域为(-1,1),
>0,且2-x≠0得F(x)的定义域为(-1,1),
设-1<x1<x2<1,则
F(x2)-F(x1)=(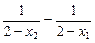 )+(
)+(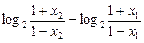 )
)
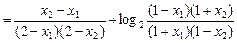 ,
,
∵x2-x1>0,2-x1>0,2-x2>0,∴上式第2项中对数的真数大于1.
因此F(x2)-F(x1)>0,F(x2)>F(x1),∴F(x)在(-1,1)上是增函数.
(2)证明: 由y=f(x)=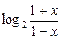 得
得 2y=
2y=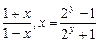 ,
,
∴f-1(x)=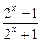 ,∵f(x)的值域为R,∴f--1(x)的定义域为R.
,∵f(x)的值域为R,∴f--1(x)的定义域为R.
当n≥3时,
f-1(n)>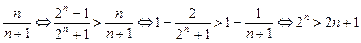 .
.
用数学归纳法易证2n>2n+1(n≥3),证略.
(3)证明:∵F(0)=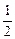 ,∴F-1(
,∴F-1(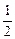 )=0,∴x=
)=0,∴x=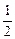 是F-1(x)=0的一个根.
是F-1(x)=0的一个根.
假设F-1(x)=0还有一个解x0(x0≠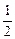 ),则F-1(x0)=0,于
),则F-1(x0)=0,于
是F(0)=x0(x0≠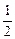 ). 这是不可能的,故F-1(x)=0有惟一解.
). 这是不可能的,故F-1(x)=0有惟一解.
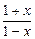 >0,且2-x≠0得F(x)的定义域为(-1,1),
>0,且2-x≠0得F(x)的定义域为(-1,1),设-1<x1<x2<1,则
F(x2)-F(x1)=(
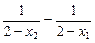 )+(
)+(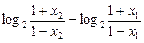 )
)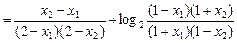 ,
,∵x2-x1>0,2-x1>0,2-x2>0,∴上式第2项中对数的真数大于1.
因此F(x2)-F(x1)>0,F(x2)>F(x1),∴F(x)在(-1,1)上是增函数.
(2)证明: 由y=f(x)=
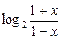 得
得 2y=
2y=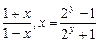 ,
,∴f-1(x)=
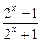 ,∵f(x)的值域为R,∴f--1(x)的定义域为R.
,∵f(x)的值域为R,∴f--1(x)的定义域为R.当n≥3时,
f-1(n)>
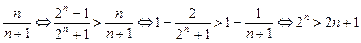 .
. 用数学归纳法易证2n>2n+1(n≥3),证略.
(3)证明:∵F(0)=
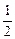 ,∴F-1(
,∴F-1(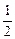 )=0,∴x=
)=0,∴x=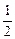 是F-1(x)=0的一个根.
是F-1(x)=0的一个根. 假设F-1(x)=0还有一个解x0(x0≠
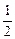 ),则F-1(x0)=0,于
),则F-1(x0)=0,于是F(0)=x0(x0≠
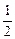 ). 这是不可能的,故F-1(x)=0有惟一解.
). 这是不可能的,故F-1(x)=0有惟一解. 
练习册系列答案
相关题目
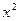 -4
-4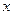 +2在点M(1,1)处的切线平行的直线方程是__________.
+2在点M(1,1)处的切线平行的直线方程是__________.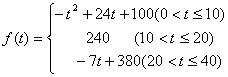
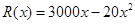 (单位:元),其成本函数为
(单位:元),其成本函数为 (单位:元),利润是收入与成本之差。
(单位:元),利润是收入与成本之差。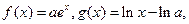 其中
其中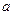 为常数,且函数
为常数,且函数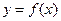 和
和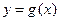 的图像在其与坐标轴的交点处的切线互相平行
的图像在其与坐标轴的交点处的切线互相平行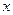 的不等式
的不等式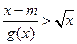 恒成立,求实数
恒成立,求实数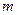 的取值范围。
的取值范围。 x2,则生产8个单位产品时,边际成 本是
x2,则生产8个单位产品时,边际成 本是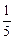 x5上一点M处的切线与直线y=3-x垂直,则此切线方程只能是
x5上一点M处的切线与直线y=3-x垂直,则此切线方程只能是 (常数
(常数 )的函数
)的函数 和
和 的图像如图所示,给出下列四个命题:
的图像如图所示,给出下列四个命题:
 有且仅有三个解;
有且仅有三个解; 有且仅有三个解;
有且仅有三个解; 有且仅有九个解;
有且仅有九个解; 有且仅有一个解。
有且仅有一个解。