题目内容
在曲线y=x3＋3x2＋6x＋10的切线中，斜率最小的切线方程是___________.
3x－y－11=0
本题考查导数的几何意义.先求导数，然后求导函数的最小值.
y′=(x3)′＋(3x2)′＋(6x)′＋10′=3x2＋6x＋6=3(x2＋2x＋2).
∴当x=－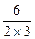
=－1时，斜率最小，最小值为3×(－1)2＋6×(－1)＋6=3.
又在曲线上当x=－1时，曲线上点的纵坐标为－14,
∴切线的方程是y＋14=3(x＋1),即3x－y－11=0.
y′=(x3)′＋(3x2)′＋(6x)′＋10′=3x2＋6x＋6=3(x2＋2x＋2).
∴当x=－
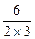=－1时，斜率最小，最小值为3×(－1)2＋6×(－1)＋6=3.又在曲线上当x=－1时，曲线上点的纵坐标为－14,
∴切线的方程是y＋14=3(x＋1),即3x－y－11=0.
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
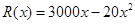（单位：元），其成本函数为
（单位：元），利润是收入与成本之差。
x2,则生产8个单位产品时，边际成 本是
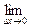
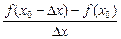的值是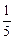
x5上一点M处的切线与直线y=3－x垂直,则此切线方程只能是
的物体按
的规律作直线运动,动能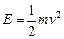
,则物体在运动
后的动能是 
表示，则该匀速运动的平均速度与任何时刻的瞬时速度（ ）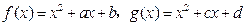
，且
，
．
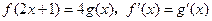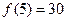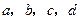的值．