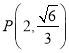题目内容
【题目】已知![]() 是关于的方程组
是关于的方程组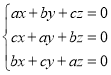 的解.
的解.
(1)求证: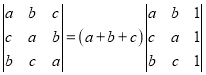 ;
;
(2)设![]() 分别为
分别为![]() 三边长,试判断
三边长,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)设![]() 为不全相等的实数,试判断
为不全相等的实数,试判断![]() 是“
是“![]() ”的 条件,并证明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
”的 条件,并证明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
【答案】(1)见解析(2)等边,见解析(3)④,见解析
【解析】
(1)将行列式的前两列加到第三列上即可得出结论;
(2)由方程组有非零解得出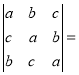 0,即
0,即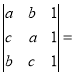 0,将行列式展开化简即可得出a=b=c;
0,将行列式展开化简即可得出a=b=c;
(3)利用(1),(2)的结论即可答案.
(1)证明:将行列式的前两列加到第三列上,
得: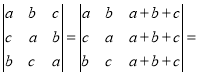 (a+b+c)
(a+b+c) .
.
(2)∵z0=1,∴方程组有非零解,
∴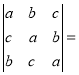 0,由(1)可知(a+b+c)
0,由(1)可知(a+b+c)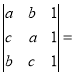 0.
0.
∵a、b、c分别为△ABC三边长,∴a+b+c≠0,
∴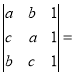 0,即a2+b2+c2﹣ab﹣bc﹣ac=0,
0,即a2+b2+c2﹣ab﹣bc﹣ac=0,
∴2a2+2b2+2c2﹣2ab﹣2bc﹣2ac=0,即(a﹣b)2+(b﹣c)2+(a﹣c)2=0,
∴a=b=c,
∴△ABC是等边三角形.
(3)若a+b+c=0,显然(0,0,0)是方程组的一组解,即x02+y02+z02=0,
∴a+b+c=0”不是“x02+y02+z02>0”的充分条件;
若x02+y02+z02>0,则方程组有非零解,
∴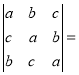 (a+b+c)
(a+b+c)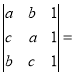 0.
0.
∴a+b+c=0或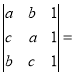 0.
0.
由(2)可知a+b+c=0或a=b=c.
∴a+b+c=0”不是“x02+y02+z02>0”的必要条件.
故答案为④.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目