ћвƒњƒЏ»Ё
°Њћвƒњ°њ“—÷™Ќ÷‘≤![]() µƒ”“љєµгќ™
µƒ”“љєµгќ™![]() £ђ«“µг
£ђ«“µг![]() ‘ЏЌ÷‘≤C…ѕ.
‘ЏЌ÷‘≤C…ѕ.
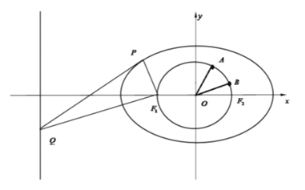
£®1£©«уЌ÷‘≤Cµƒ±к„ЉЈљ≥ћ£ї
£®2£©єэЌ÷‘≤ …ѕ“м”Џ∆дґ•µгµƒ»ќ“в“їµгQ„ч‘≤
…ѕ“м”Џ∆дґ•µгµƒ»ќ“в“їµгQ„ч‘≤![]() µƒЅљћх«–ѕя£ђ«–µгЈ÷±рќ™
µƒЅљћх«–ѕя£ђ«–µгЈ÷±рќ™![]() ≤ї‘Џ„ш±к÷б…ѕ£©£ђ»ф÷±ѕя
≤ї‘Џ„ш±к÷б…ѕ£©£ђ»ф÷±ѕя![]() ‘Џx÷б£ђy÷б…ѕµƒљЎЊаЈ÷±рќ™
‘Џx÷б£ђy÷б…ѕµƒљЎЊаЈ÷±рќ™![]() £ђ÷§√ч£Ї
£ђ÷§√ч£Ї![]() ќ™ґ®÷µ£ї
ќ™ґ®÷µ£ї
£®3£©»ф![]() «Ќ÷‘≤
«Ќ÷‘≤![]() …ѕ≤їЌђЅљµг£ђ
…ѕ≤їЌђЅљµг£ђ![]() ÷б£ђ‘≤Eєэ
÷б£ђ‘≤Eєэ![]() £ђ«“Ќ÷‘≤
£ђ«“Ќ÷‘≤![]() …ѕ»ќ“в“їµгґЉ≤ї‘Џ‘≤EƒЏ£ђ‘т≥∆‘≤Eќ™Є√Ќ÷‘≤µƒ“їЄцƒЏ«–‘≤£ђ ‘ќ £ЇЌ÷‘≤
…ѕ»ќ“в“їµгґЉ≤ї‘Џ‘≤EƒЏ£ђ‘т≥∆‘≤Eќ™Є√Ќ÷‘≤µƒ“їЄцƒЏ«–‘≤£ђ ‘ќ £ЇЌ÷‘≤![]() «Јсіж‘ЏєэљєµгFµƒƒЏ«–‘≤£њ»фіж‘Џ£ђ«у≥ц‘≤–ƒEµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
«Јсіж‘ЏєэљєµгFµƒƒЏ«–‘≤£њ»фіж‘Џ£ђ«у≥ц‘≤–ƒEµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©÷§√чЉыљвќц£ї£®3£©
£ї£®2£©÷§√чЉыљвќц£ї£®3£© .
.
°Њљвќц°њ
£®1£©”…љєµг„ш±к»Јґ®≥цcµƒ÷µ£ђЄщЊЁЌ÷‘≤µƒ–‘÷ Ѕ–≥цa”лbµƒЈљ≥ћ£ђ‘ўљЂPµг„ш±кіъ»лЌ÷‘≤Јљ≥ћЅ–≥цєЎ”Џa”лbµƒЈљ≥ћ£ђЅ™ЅҐ«у≥цa”лbµƒ÷µ£ђ»Јґ®≥цЌ÷‘≤Јљ≥ћЉіњ…£Ѓ
£®2£©”…ћв“в£Ї»Јґ®≥цC1µƒЈљ≥ћ£ђ…иµгP£®x1£ђy1£©£ђM£®x2£ђy2£©£ђN£®x3£ђy3£©£ђЄщЊЁM£ђN≤ї‘Џ„ш±к÷б…ѕ£ђµ√µљ÷±ѕяPM”л÷±ѕяOM–±¬ ≥Ћїэќ™©Б1£ђ»Јґ®≥ц÷±ѕяPMµƒЈљ≥ћ£ђЌђјнњ…µ√÷±ѕяPNµƒЈљ≥ћ£ђљшґш»Јґ®≥ц÷±ѕяMNЈљ≥ћ£ђ«у≥ц÷±ѕяMN”лx÷б£ђy÷бљЎЊаm”лn£ђЉіњ…»Јґ®≥цЋщ«у љ„”µƒ÷µќ™ґ®÷µ£Ѓ
£®3£©“јћв“вњ…µ√ЈыЇѕ“™«уµƒ‘≤E£ђЉіќ™єэµгF£ђP1£ђP2µƒ»эљ«–ќµƒЌвљ”‘≤£ЃЋщ“‘‘≤–ƒ‘Џx÷б…ѕ£ЃЄщЊЁћв“в–і≥ц‘≤EµƒЈљ≥ћ£Ѓ”…”Џ‘≤µƒіж‘Џ±Ў–л“™ЈыЇѕ£ђЌ÷‘≤…ѕµƒµгµљ‘≤EЊајлµƒ„о–°÷µ «|P1E|£ђљбЇѕЌЉ–ќњ…µ√‘≤–ƒE‘ЏѕяґќP1P2…ѕ£ђ∞лЊґ„о–°£Ѓ”÷”…”ЏµгF“—÷™£ђЉіњ…«уµ√љб¬џ£Ѓ
£®1£©°яЌ÷‘≤C£Ї![]() µƒ”“љєµгќ™F£®1£ђ0£©£ђ«“µгP£®1,
µƒ”“љєµгќ™F£®1£ђ0£©£ђ«“µгP£®1,![]() £©‘ЏЌ÷‘≤C…ѕ£ї
£©‘ЏЌ÷‘≤C…ѕ£ї
°а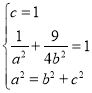 £ђљвµ√a£љ2£ђb£љ
£ђљвµ√a£љ2£ђb£љ![]() £ђ
£ђ
°аЌ÷‘≤Cµƒ±к„ЉЈљ≥ћќ™![]() £Ѓ
£Ѓ
£®2£©”…ћв“в£ЇC1£Ї![]() £ђ
£ђ
…иµгP£®x1£ђy1£©£ђM£®x2£ђy2£©£ђN£®x3£ђy3£©£ђ
°яM£ђN≤ї‘Џ„ш±к÷б…ѕ£ђ°аkPM£љ©Б![]() £љ©Б
£љ©Б![]() £ђ
£ђ
°а÷±ѕяPMµƒЈљ≥ћќ™y©Бy2£љ©Б![]() £®x©Бx2£©£ђ
£®x©Бx2£©£ђ
їѓЉтµ√£Їx2x+y2y£љ![]() £ђҐў£ђ
£ђҐў£ђ
Ќђјнњ…µ√÷±ѕяPNµƒЈљ≥ћќ™x3x+y3y£љ![]() £ђҐЏ£ђ
£ђҐЏ£ђ
∞—Pµгµƒ„ш±кіъ»лҐў°ҐҐЏµ√ £ђ
£ђ
°а÷±ѕяMNµƒЈљ≥ћќ™x1x+y1y£љ![]() £ђ
£ђ
Ѕоy£љ0£ђµ√m£љ![]() £ђЅоx£љ0µ√n£љ
£ђЅоx£љ0µ√n£љ![]() £ђ
£ђ
°аx1£љ![]() £ђy1£љ
£ђy1£љ![]() £ђ
£ђ
”÷µгP‘ЏЌ÷‘≤C1…ѕ£ђ
°а£®![]() £©2+3£®
£©2+3£®![]() £©2£љ4£ђ
£©2£љ4£ђ
‘т![]() £љ
£љ![]() ќ™ґ®÷µ£Ѓ
ќ™ґ®÷µ£Ѓ
£®3£©”…Ќ÷‘≤µƒґ‘≥∆–‘£ђњ…“‘…иP1£®m£ђn£©£ђP2£®m£ђ©Бn£©£ђµгE‘Џx÷б…ѕ£ђ…иµгE£®t£ђ0£©£ђ
‘т‘≤EµƒЈљ≥ћќ™£Ї£®x©Бt£©2+y2£љ£®m©Бt£©2+n2£ђ
”…ƒЏ«–‘≤ґ®“е÷™µј£ђЌ÷‘≤…ѕµƒµгµљµгEЊајлµƒ„о–°÷µ «|P1E|£ђ
…иµгM£®x£ђy£© «Ќ÷‘≤C…ѕ»ќ“в“їµг£ђ‘т|ME|2£љ£®x©Бt£©2+y2£љ![]() £ђ
£ђ
µ±x£љm ±£ђ|ME|2„о–°£ђ°аm£љ©Б![]() £ђҐџ£ђ
£ђҐџ£ђ
”÷‘≤EєэµгF£ђ°а£®©Б![]() £©2£љ£®m©Бt£©2+n2£ђҐ№
£©2£љ£®m©Бt£©2+n2£ђҐ№
µгP1‘ЏЌ÷‘≤…ѕ£ђ°а![]() £ђҐЁ
£ђҐЁ
”…ҐџҐ№ҐЁ£ђљвµ√£Їt£љ©Б![]() їтt£љ©Б
їтt£љ©Б![]() £ђ
£ђ
”÷t£љ©Б![]() ±£ђm£љ©Б
±£ђm£љ©Б![]() £Љ©Б2£ђ≤їЇѕћв“в£ђ
£Љ©Б2£ђ≤їЇѕћв“в£ђ
„џ…ѕ£ЇЌ÷‘≤Cіж‘ЏЈыЇѕћхЉюµƒƒЏ«–‘≤£ђµгEµƒ„ш±к «£®©Б![]() £ђ0£©£Ѓ
£ђ0£©£Ѓ

 ÷«»§ оЉўќ¬є ÷™–¬ѕµЅ–ір∞Є
÷«»§ оЉўќ¬є ÷™–¬ѕµЅ–ір∞Є ”Ґ”п–°”Ґ–џћмћмƒђ–іѕµЅ–ір∞Є
”Ґ”п–°”Ґ–џћмћмƒђ–іѕµЅ–ір∞Є оЉў„ч“µ∞≤ї’…ўƒкґщЌѓ≥ц∞ж…зѕµЅ–ір∞Є
оЉў„ч“µ∞≤ї’…ўƒкґщЌѓ≥ц∞ж…зѕµЅ–ір∞Є