题目内容
(本小题12分)离心率为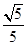 的椭圆
的椭圆 :
: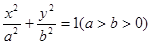 的左、右焦点分别为
的左、右焦点分别为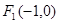 、
、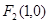 ,
,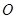 是坐标原点.
是坐标原点.
(1)求椭圆 的方程;
的方程;
(2)若直线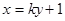 与
与 交于相异两点
交于相异两点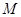 、
、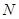 ,且
,且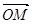

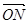
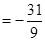 ,求
,求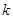 .(其中
.(其中 是坐标原点)
是坐标原点)
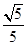 的椭圆
的椭圆 :
: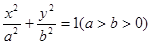 的左、右焦点分别为
的左、右焦点分别为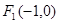 、
、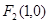 ,
,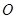 是坐标原点.
是坐标原点.(1)求椭圆
 的方程;
的方程; (2)若直线
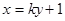 与
与 交于相异两点
交于相异两点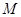 、
、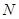 ,且
,且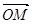

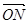
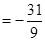 ,求
,求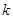 .(其中
.(其中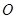 是坐标原点)
是坐标原点)(1)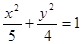 ;(Ⅱ)
;(Ⅱ)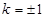 。
。
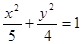 ;(Ⅱ)
;(Ⅱ)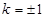 。
。本题考查的知识点是直线与圆的位置关系,直线与圆锥曲线的综合应用,其中根据已知条件求出椭圆的标准方程是解答本题的关键.
(1)利用椭圆的几何性质可知道参数a,b,c的值,进而求解得到。
(2)由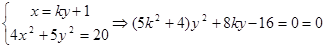
结合韦达定理得到向量的关系式以及参数k的值。
解:(1)依题意得
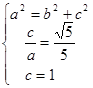 ----------------3分
----------------3分
解得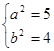 ,故椭圆
,故椭圆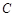 的方程为
的方程为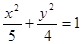 --------------6分
--------------6分
(Ⅱ)由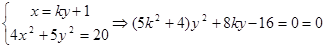 --------------7分
--------------7分
设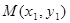 ,
,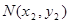 则
则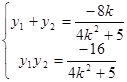 ------------8分
------------8分
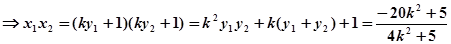
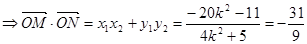 -----------------10分
-----------------10分
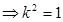 ,从而
,从而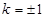 。----------------- 12分
。----------------- 12分
(1)利用椭圆的几何性质可知道参数a,b,c的值,进而求解得到。
(2)由
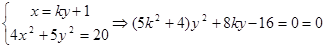
结合韦达定理得到向量的关系式以及参数k的值。
解:(1)依题意得
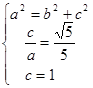 ----------------3分
----------------3分解得
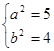 ,故椭圆
,故椭圆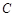 的方程为
的方程为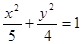 --------------6分
--------------6分(Ⅱ)由
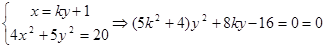 --------------7分
--------------7分设
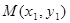 ,
,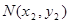 则
则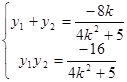 ------------8分
------------8分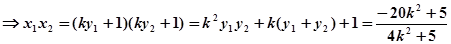
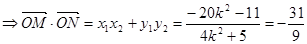 -----------------10分
-----------------10分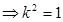 ,从而
,从而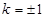 。----------------- 12分
。----------------- 12分
练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
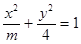 ,对于任意实数
,对于任意实数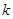 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线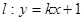 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )

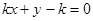


 经过点
经过点 ,一个焦点是
,一个焦点是 .
. 的方程;
的方程; 轴的两个交点为
轴的两个交点为 、
、 ,点
,点 在直线
在直线 上,直线
上,直线 、
、 分别与椭圆
分别与椭圆 、
、 两点.试问:当点
两点.试问:当点 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.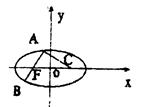
 经过点(0,1),离心率
经过点(0,1),离心率 。
。 与椭圆C交于A、B两点,点A关于x轴的对称点为
与椭圆C交于A、B两点,点A关于x轴的对称点为 。
。 的面积关于m的函数关系;
的面积关于m的函数关系; 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
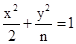 的离心率为
的离心率为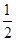 ,则n=( )
,则n=( )



 上一点P到焦点F1的距离为7,则点P到F2相对应的准线的距离是____;
上一点P到焦点F1的距离为7,则点P到F2相对应的准线的距离是____; 的左、右焦点分别为
的左、右焦点分别为 ,
, 是双曲线上一点,
是双曲线上一点,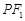 的中点
的中点 轴上,线段
轴上,线段 的长为
的长为 ,则该双曲线的离心率为
,则该双曲线的离心率为


