题目内容
双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, 是双曲线上一点,
是双曲线上一点,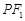 的中点
的中点
在 轴上,线段
轴上,线段 的长为
的长为 ,则该双曲线的离心率为
,则该双曲线的离心率为
 的左、右焦点分别为
的左、右焦点分别为 ,
, 是双曲线上一点,
是双曲线上一点,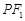 的中点
的中点在
 轴上,线段
轴上,线段 的长为
的长为 ,则该双曲线的离心率为
,则该双曲线的离心率为A. | B. | C. | D. |
D
由题意可知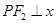 轴,所以
轴,所以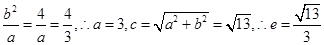 .
.
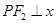 轴,所以
轴,所以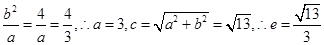 .
.
练习册系列答案
相关题目
题目内容
 的左、右焦点分别为
的左、右焦点分别为 ,
, 是双曲线上一点,
是双曲线上一点, 的中点
的中点 轴上,线段
轴上,线段 的长为
的长为 ,则该双曲线的离心率为
,则该双曲线的离心率为A. | B. | C. | D. |
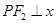 轴,所以
轴,所以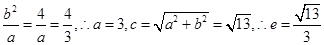 .
.