题目内容
椭圆E: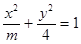 ,对于任意实数
,对于任意实数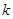 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线
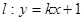 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )
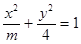 ,对于任意实数
,对于任意实数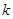 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线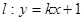 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )A. | B. | C.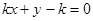 | D. |
D
本题考查直线和椭圆的位置关系,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.
由数形结合可知,当l过点(-1,0)时,直线l和选项A中的直线重合,故不能选 A.
当l过点(1,0)时,直线l和选项D中的直线关于y轴对称,被椭圆E所截得的弦长相同,故不能选D.
当k=0时,直线l和选项B中的直线关于x轴对称,被椭圆E所截得的弦长相同,故不能选B.
直线l斜率为k,在y轴上的截距为1;选项C中的直线kx+y-2="0" 斜率为-k,在y轴上的截距为2,这两直线不关于x轴、
y轴、原点对称,故被椭圆E所截得的弦长不可能相等,故选D
解决该试题的关键是对l过点(-1,0)时, 或者过点(1,0)时, 当k=0时,直线l和选项B中的直线关于x轴对称,被椭圆E所截得的弦长相同.讨论得到。
由数形结合可知,当l过点(-1,0)时,直线l和选项A中的直线重合,故不能选 A.
当l过点(1,0)时,直线l和选项D中的直线关于y轴对称,被椭圆E所截得的弦长相同,故不能选D.
当k=0时,直线l和选项B中的直线关于x轴对称,被椭圆E所截得的弦长相同,故不能选B.
直线l斜率为k,在y轴上的截距为1;选项C中的直线kx+y-2="0" 斜率为-k,在y轴上的截距为2,这两直线不关于x轴、
y轴、原点对称,故被椭圆E所截得的弦长不可能相等,故选D
解决该试题的关键是对l过点(-1,0)时, 或者过点(1,0)时, 当k=0时,直线l和选项B中的直线关于x轴对称,被椭圆E所截得的弦长相同.讨论得到。

练习册系列答案
相关题目
 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点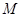 (2,1),平行于
(2,1),平行于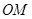 直线
直线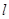 在
在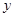 轴上的截距为
轴上的截距为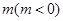 ,设直线
,设直线 、
、 ,
,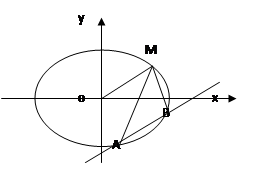
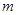 的允许值,
的允许值,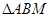 的内心在定直线
的内心在定直线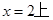 。
。 上一点
上一点 到焦点
到焦点 的距离为2,
的距离为2, 是
是 的中点,则
的中点,则 等于( )
等于( )


 PD.
PD.
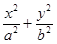 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e=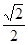 ,且经过点(
,且经过点(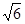 ,1),O为坐标原点。
,1),O为坐标原点。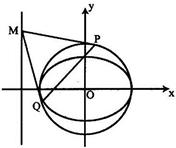
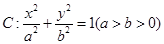 的长轴长是短轴长的两倍,且过点
的长轴长是短轴长的两倍,且过点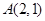
 的标准方程;
的标准方程;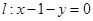 与椭圆
与椭圆 ,求
,求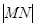 的值.
的值.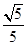 的椭圆
的椭圆 :
: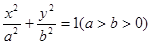 的左、右焦点分别为
的左、右焦点分别为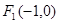 、
、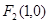 ,
, 是坐标原点.
是坐标原点. 与
与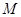 、
、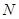 ,且
,且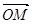

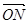
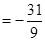 ,求
,求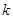 .(其中
.(其中 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,| P F1|=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,| P F1|= ,| P F2|=
,| P F2|=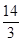 。
。