题目内容
(本题满分15分 )已知椭圆
 经过点
经过点 ,一个焦点是
,一个焦点是 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 与
与 轴的两个交点为
轴的两个交点为 、
、 ,点
,点 在直线
在直线 上,直线
上,直线 、
、 分别与椭圆
分别与椭圆 交于
交于 、
、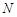 两点.试问:当点
两点.试问:当点 在直线
在直线 上运动时,直线
上运动时,直线 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.

 经过点
经过点 ,一个焦点是
,一个焦点是 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设椭圆
 与
与 轴的两个交点为
轴的两个交点为 、
、 ,点
,点 在直线
在直线 上,直线
上,直线 、
、 分别与椭圆
分别与椭圆 交于
交于 、
、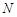 两点.试问:当点
两点.试问:当点 在直线
在直线 上运动时,直线
上运动时,直线 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.I)
(II)当点 在直线
在直线 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点 .
.

(II)当点
 在直线
在直线 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点 .
.(I)由题意可知椭圆的两个焦点的坐标分别为 ,再根据椭圆过点
,再根据椭圆过点 ,由椭圆的定义可求出
,由椭圆的定义可求出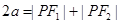 ,利用
,利用 ,求出b,焦点在y轴上,所以椭圆方程确定.
,求出b,焦点在y轴上,所以椭圆方程确定.
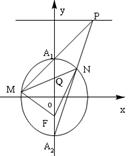
(2)分两种情况研究此问题:当点 在
在 轴上时,
轴上时, 、
、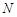 分别与
分别与 、
、 重合,
重合,
若直线 通过定点
通过定点 ,则
,则 必在
必在 轴上,设
轴上,设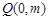 ,当点
,当点 不在
不在 轴上时,设
轴上时,设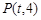 ,
,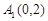 、
、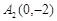 ,
,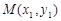 ,
,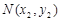 ,然后分别表示出PA1和PA2的方程,分别与椭圆C方程联立求出M,N的坐标,进而得到向量
,然后分别表示出PA1和PA2的方程,分别与椭圆C方程联立求出M,N的坐标,进而得到向量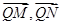 的坐标,再根据
的坐标,再根据
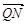 ,得到
,得到 ,因而求出m=1,从而得到定点Q(1,0).
,因而求出m=1,从而得到定点Q(1,0).
I)方法1:椭圆的一个焦点是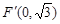 ,
,

(II)当点 在
在 轴上时,
轴上时, 、
、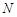 分别与
分别与 、
、 重合,
重合,
若直线 通过定点
通过定点 ,则
,则 必在
必在 轴上,设
轴上,设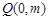 ,………………(6分)
,………………(6分)
当点 不在
不在 轴上时,设
轴上时,设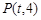 ,
,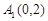 、
、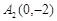 ,
,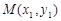 ,
,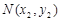
直线 方程
方程 ,
, 方程
方程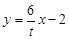 ,
,
 代入
代入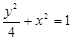 得
得 ,
,
解得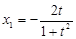 ,
,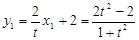 ,
,
∴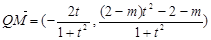 , ……………(9分)
, ……………(9分)
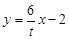 代入
代入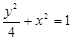 得
得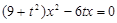
解得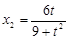 ,
, ,
,
∴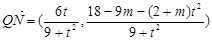 , ………………(11分)
, ………………(11分)
∵
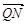 ,
,
∴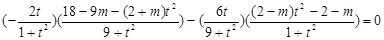 ,
,
∴ ,
,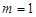 ,
,
∴当点 在直线
在直线 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点 .……(15分)
.……(15分)
 ,再根据椭圆过点
,再根据椭圆过点 ,由椭圆的定义可求出
,由椭圆的定义可求出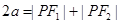 ,利用
,利用 ,求出b,焦点在y轴上,所以椭圆方程确定.
,求出b,焦点在y轴上,所以椭圆方程确定.(2)分两种情况研究此问题:当点
 在
在 轴上时,
轴上时, 、
、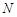 分别与
分别与 、
、 重合,
重合,若直线
 通过定点
通过定点 ,则
,则 必在
必在 轴上,设
轴上,设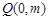 ,当点
,当点 不在
不在 轴上时,设
轴上时,设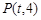 ,
,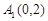 、
、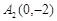 ,
,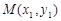 ,
,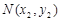 ,然后分别表示出PA1和PA2的方程,分别与椭圆C方程联立求出M,N的坐标,进而得到向量
,然后分别表示出PA1和PA2的方程,分别与椭圆C方程联立求出M,N的坐标,进而得到向量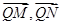 的坐标,再根据
的坐标,再根据
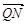 ,得到
,得到 ,因而求出m=1,从而得到定点Q(1,0).
,因而求出m=1,从而得到定点Q(1,0).I)方法1:椭圆的一个焦点是
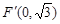 ,
,
(II)当点
 在
在 轴上时,
轴上时, 、
、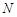 分别与
分别与 、
、 重合,
重合,若直线
 通过定点
通过定点 ,则
,则 必在
必在 轴上,设
轴上,设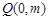 ,………………(6分)
,………………(6分)当点
 不在
不在 轴上时,设
轴上时,设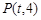 ,
,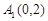 、
、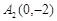 ,
,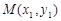 ,
,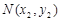

直线
 方程
方程 ,
, 方程
方程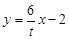 ,
, 代入
代入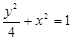 得
得 ,
,解得
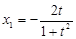 ,
,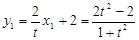 ,
,∴
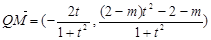 , ……………(9分)
, ……………(9分)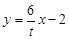 代入
代入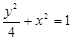 得
得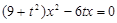
解得
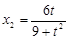 ,
, ,
, ∴
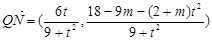 , ………………(11分)
, ………………(11分)∵

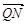 ,
,∴
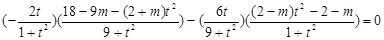 ,
,∴
 ,
,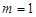 ,
,∴当点
 在直线
在直线 上运动时,直线
上运动时,直线 恒经过定点
恒经过定点 .……(15分)
.……(15分)
练习册系列答案
相关题目
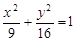 一动点P到两焦点距离之和为( )
一动点P到两焦点距离之和为( ) PD.
PD.
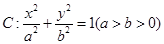 的长轴长是短轴长的两倍,且过点
的长轴长是短轴长的两倍,且过点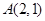
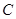 的标准方程;
的标准方程;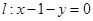 与椭圆
与椭圆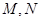 ,求
,求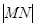 的值.
的值.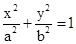 (a>b>0)的离心率为
(a>b>0)的离心率为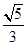 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.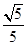 的椭圆
的椭圆 :
: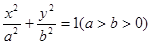 的左、右焦点分别为
的左、右焦点分别为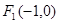 、
、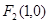 ,
,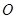 是坐标原点.
是坐标原点.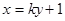 与
与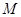 、
、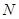 ,且
,且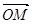

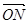
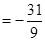 ,求
,求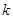 .(其中
.(其中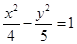 的焦点为顶点,顶点为焦点的椭圆的方程为
的焦点为顶点,顶点为焦点的椭圆的方程为