题目内容
(14分)已知椭圆 经过点(0,1),离心率
经过点(0,1),离心率 。
。
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于A、B两点,点A关于x轴的对称点为
与椭圆C交于A、B两点,点A关于x轴的对称点为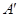 。
。
①试建立 的面积关于m的函数关系;
的面积关于m的函数关系;
②某校高二(1)班数学兴趣小组通过试验操作初步推断;“当m变化时,直线 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
 经过点(0,1),离心率
经过点(0,1),离心率 。
。(1)求椭圆C的方程;
(2)设直线
 与椭圆C交于A、B两点,点A关于x轴的对称点为
与椭圆C交于A、B两点,点A关于x轴的对称点为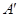 。
。①试建立
 的面积关于m的函数关系;
的面积关于m的函数关系;②某校高二(1)班数学兴趣小组通过试验操作初步推断;“当m变化时,直线
 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
(1)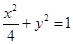 ;
;
(2)①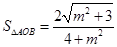 ;②正确,
;②正确,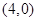
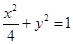 ;
;(2)①
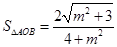 ;②正确,
;②正确,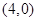
本试题主要是考查了椭圆的方程以及性质的运用,以及直线与椭圆的位置关系的综合运用。
(1)因为椭圆 经过点(0,1),离心率
经过点(0,1),离心率 ,利用a,b,c得到椭圆的方程。
,利用a,b,c得到椭圆的方程。
(2)联立方程组 ,结合韦达定理得到根与系数的关系,表示三角形的面积,进而得到定值的求解。
,结合韦达定理得到根与系数的关系,表示三角形的面积,进而得到定值的求解。
解:(1)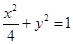 ……(3分)
……(3分)
(2)①设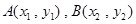
由 得
得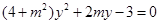
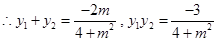
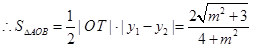 ……(8分)
……(8分)
②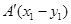
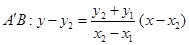
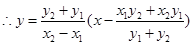
令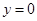 则
则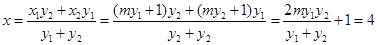 为定值。(14分)
为定值。(14分)
(1)因为椭圆
 经过点(0,1),离心率
经过点(0,1),离心率 ,利用a,b,c得到椭圆的方程。
,利用a,b,c得到椭圆的方程。(2)联立方程组
 ,结合韦达定理得到根与系数的关系,表示三角形的面积,进而得到定值的求解。
,结合韦达定理得到根与系数的关系,表示三角形的面积,进而得到定值的求解。解:(1)
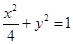 ……(3分)
……(3分)(2)①设
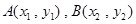
由
 得
得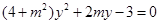
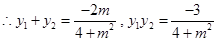
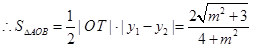 ……(8分)
……(8分)②
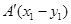
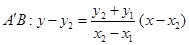
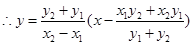
令
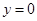 则
则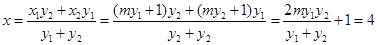 为定值。(14分)
为定值。(14分)
练习册系列答案
相关题目
 :
: 的离心率为
的离心率为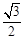 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. ,
, 、
、 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,求直线
,求直线 与
与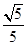 的椭圆
的椭圆 :
: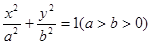 的左、右焦点分别为
的左、右焦点分别为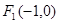 、
、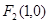 ,
,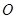 是坐标原点.
是坐标原点.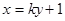 与
与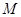 、
、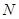 ,且
,且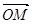

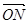
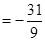 ,求
,求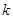 .(其中
.(其中 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,| P F1|=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,| P F1|= ,| P F2|=
,| P F2|=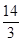 。
。 上任一点P,由点P向x轴作垂线段PQ,垂足为Q,点M在PQ上,且
上任一点P,由点P向x轴作垂线段PQ,垂足为Q,点M在PQ上,且 ,点M的轨迹为C.
,点M的轨迹为C. 且平行于
且平行于 轴的直线上一动点,满足
轴的直线上一动点,满足 (O为原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线的方程;若不存在说明理由.
(O为原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线的方程;若不存在说明理由.
 是椭圆的一部分,灯丝位于椭圆的一个焦点
是椭圆的一部分,灯丝位于椭圆的一个焦点 上,片门位于另一个焦点
上,片门位于另一个焦点 上,由椭圆一个焦点
上,由椭圆一个焦点 ,
, ,
, 试建立适当的坐标系,求截口
试建立适当的坐标系,求截口 的一个焦点为F(2,0),离心率
的一个焦点为F(2,0),离心率 .
. 与椭圆交于不同的A,B两点,与y轴交于E点,且
与椭圆交于不同的A,B两点,与y轴交于E点,且 ,求实数m的值.
,求实数m的值.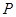 是椭圆
是椭圆 上一点,
上一点, 和
和 是椭圆的两个焦点,则
是椭圆的两个焦点,则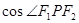 的最小值是( )
的最小值是( )


