题目内容
已知椭圆的长轴长是短轴长的2倍且经过点A(2,0),求椭圆的标准方程。
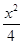 +y2=1或
+y2=1或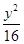 +
+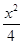 =1.
=1.本试题主要是考查了椭圆的性质以及根据性质求解椭圆的方程的综合运用。因为椭圆的长轴长是短轴长的2倍且经过点A(2,0),那么设出椭圆的方程,然后结合已知中的条件,得到参数a,b的值,进而求解椭圆方程。
解:(1)若椭圆的焦点在x轴上,设方程为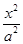 +
+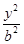 =1(a>b>0),
=1(a>b>0),
∵椭圆过点A(2,0),∴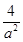 =1,a=2,∵2a=2·2b,∴b=1,∴方程为
=1,a=2,∵2a=2·2b,∴b=1,∴方程为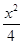 +y2=1.
+y2=1.
若椭圆的焦点在y轴上,设椭圆方程为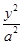 +
+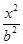 =1(a>b>0),
=1(a>b>0),
∵椭圆过点A(2,0),∴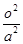 +
+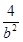 =1,∴b=2,2a=2·2b,∴a=4,∴方程为
=1,∴b=2,2a=2·2b,∴a=4,∴方程为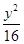 +
+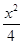 =1.
=1.
综上所述,椭圆方程为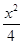 +y2=1或
+y2=1或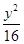 +
+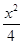 =1.
=1.
解:(1)若椭圆的焦点在x轴上,设方程为
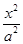 +
+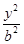 =1(a>b>0),
=1(a>b>0),∵椭圆过点A(2,0),∴
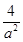 =1,a=2,∵2a=2·2b,∴b=1,∴方程为
=1,a=2,∵2a=2·2b,∴b=1,∴方程为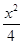 +y2=1.
+y2=1.若椭圆的焦点在y轴上,设椭圆方程为
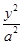 +
+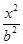 =1(a>b>0),
=1(a>b>0),∵椭圆过点A(2,0),∴
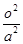 +
+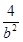 =1,∴b=2,2a=2·2b,∴a=4,∴方程为
=1,∴b=2,2a=2·2b,∴a=4,∴方程为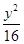 +
+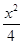 =1.
=1.综上所述,椭圆方程为
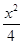 +y2=1或
+y2=1或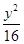 +
+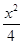 =1.
=1.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,斜率为
,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,且点
两点,且点 在直线
在直线 轴交点的横坐标
轴交点的横坐标 的取值范围;
的取值范围; 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 
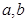 是方程x
是方程x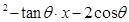 =0的两个实根,那么过点
=0的两个实根,那么过点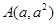 和
和 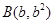 (
(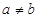 )的直线与椭圆
)的直线与椭圆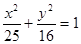 的位置关系是
的位置关系是 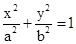 (a>b>0)的离心率为
(a>b>0)的离心率为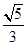 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.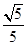 的椭圆
的椭圆 :
: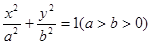 的左、右焦点分别为
的左、右焦点分别为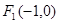 、
、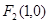 ,
,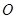 是坐标原点.
是坐标原点.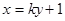 与
与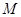 、
、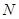 ,且
,且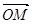

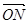
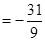 ,求
,求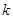 .(其中
.(其中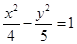 的焦点为顶点,顶点为焦点的椭圆的方程为
的焦点为顶点,顶点为焦点的椭圆的方程为  ∈(0,
∈(0, ),方程
),方程 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则


 是椭圆的一部分,灯丝位于椭圆的一个焦点
是椭圆的一部分,灯丝位于椭圆的一个焦点 上,片门位于另一个焦点
上,片门位于另一个焦点 上,由椭圆一个焦点
上,由椭圆一个焦点 ,
, ,
, 试建立适当的坐标系,求截口
试建立适当的坐标系,求截口