题目内容
(本小题满分15分)已知函数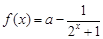 ,
,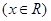 .
.
(1)用定义证明:不论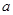 为何实数
为何实数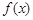 在
在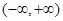 上为增函数;
上为增函数;
(2)若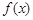 为奇函数,求
为奇函数,求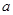 的值;
的值;
(3)在(2)的条件下,求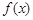 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
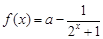 ,
,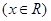 .
.(1)用定义证明:不论
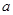 为何实数
为何实数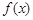 在
在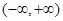 上为增函数;
上为增函数;(2)若
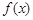 为奇函数,求
为奇函数,求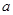 的值;
的值;(3)在(2)的条件下,求
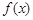 在区间[1,5]上的最小值.
在区间[1,5]上的最小值. (1)见解析;(2) ;(3)
;(3) .
.
 ;(3)
;(3) .
.试题分析:(1)
 的定义域为R, 任取
的定义域为R, 任取 ,------------1分
,------------1分则
 =
=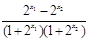 . -----------3分
. -----------3分 ,∴
,∴  .
.∴
 ,即
,即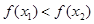 .
.所以不论
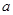 为何实数
为何实数 总为增函数.————————5分
总为增函数.————————5分(2)
 在
在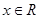 上为奇函数,
上为奇函数, ∴
 , ------------7分
, ------------7分即
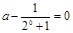 .解得
.解得  . —————————————10分
. —————————————10分(3)由(2)知,
 ,
, 由(1) 知,
 为增函数,
为增函数,∴
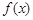 在区间
在区间 上的最小值为
上的最小值为 . ------------13分
. ------------13分∵
 ,
,∴
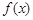 在区间
在区间 上的最小值为
上的最小值为 .———————————————15分
.———————————————15分点评:(1)用的定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论。
(2)灵活应用奇函数的性质:若x=0在函数的定义域内,则f(0)=0。属于基础试题。

练习册系列答案
相关题目
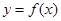 是定义在
是定义在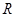 上的奇函数,当
上的奇函数,当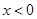 时,
时,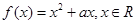 ,且
,且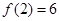 ,则
,则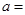 .
.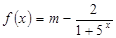 。
。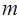 ,使
,使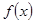 是奇函数?若存在,求出
是奇函数?若存在,求出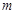 的值;若不存在,给出证明。
的值;若不存在,给出证明。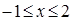 时,
时,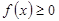 恒成立,求实数
恒成立,求实数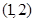 内是增函数的为( )
内是增函数的为( )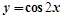
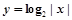
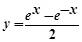
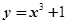
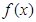 是定义在
是定义在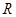 上的奇函数,当
上的奇函数,当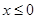 时,
时,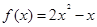 ,则
,则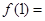
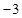
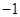
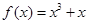 的奇偶性是 .
的奇偶性是 .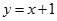
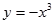
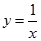
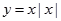
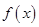 在
在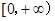 上是减函数,求不等式
上是减函数,求不等式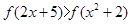 的解集。
的解集。