题目内容
下列函数中,既是奇函数又是增函数的为
A.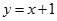 | B.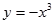 | C.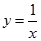 | D.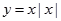 |
D
试题分析:奇函数需要满足两个条件:1、定义域关于原点对称,2、
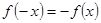
奇函数的性质:1、图像关于原点对称,2、关于观点对称的两个区间上函数图像的单调性相同,3、当函数在
 处有定义时,满足
处有定义时,满足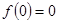 ,故可以首先排除A选择,其不是奇函数,而B选项是奇函数却是R上的减函数, C选项是奇函数,且在区间
,故可以首先排除A选择,其不是奇函数,而B选项是奇函数却是R上的减函数, C选项是奇函数,且在区间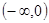 ,区间
,区间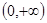 上都单调增,但在整个定义域上不具有单调性,由排除法就可选出正确答案D,当然D选项可以转化成分段函数
上都单调增,但在整个定义域上不具有单调性,由排除法就可选出正确答案D,当然D选项可以转化成分段函数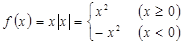 ,数形结合同样可以得到正确答案。
,数形结合同样可以得到正确答案。点评:本题学生可能忽略单调性的函数的局部性质这一特点,误选C项而造成失分。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
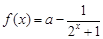 ,
,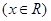 .
.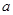 为何实数
为何实数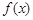 在
在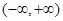 上为增函数;
上为增函数;
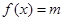 有两个根,试求
有两个根,试求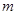 的取值范围。
的取值范围。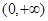 上单调递减的是( )
上单调递减的是( )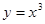
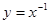
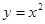
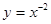
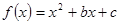 ,且
,且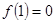
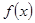 是偶函数,求
是偶函数,求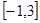 上的最大、最小值;(3分)
上的最大、最小值;(3分)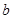 的范围。(4分)
的范围。(4分)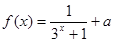 是奇函数,则实数
是奇函数,则实数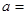
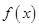 的定义域为R,当
的定义域为R,当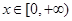 时
时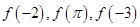 的大小关系是( )
的大小关系是( )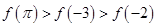
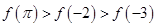
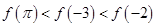
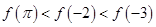
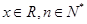 ,定义:
,定义: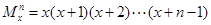 ,例如
,例如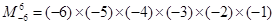 ,则函数
,则函数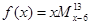
 为偶函数,则实数
为偶函数,则实数