题目内容
【题目】在平面直角坐标系xOy中，椭圆C: 
=1（a>b>0）过点P(1, 
）．离心率为
．
(1)求椭圆C的方程；
(2)设直线l与椭圆C交于A，B两点．
①若直线l过椭圆C的右焦点，记△ABP三条边所在直线的斜率的乘积为t．
求t的最大值；
②若直线l的斜率为
，试探究OA2+ OB2是否为定值，若是定值，则求出此
定值；若不是定值，请说明理由．
【答案】（1）
（2）当
时，t有最大值
；定值7
【解析】试题分析: （1）由椭圆过点P(1, 
），离心率为
，列出方程组，求出a，b，由此能求出椭圆C的方程．
（2）①设直线l的方程为x=my+1，代入椭圆，得（3m2+4）y2+6my﹣9=0，由此利用根的判别式、韦达定理，结合已知条件能求出t的最大值．
②设直线l的方程为
，代入椭圆，得
，由此利用根的判别式、韦达定理，结合已知条件能求出OA2+OB2为定值．
试题解析：
（1）
得
所以椭圆
.
（2）①设直线l的方程为
，直线l与椭圆C的交点为
，
由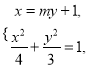
化简得
，易知
，
所以
，
所以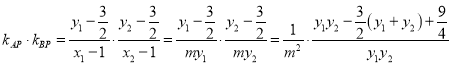
＝
，
所以
，
所以当
时，t有最大值
.
②设直线l的方程为
，直线l与椭圆C的交点为
，
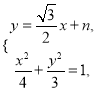得
，
，即
.
，
，
=
=
=
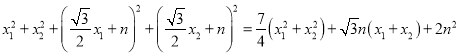
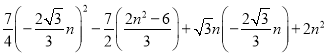=7.
手拉手全优练考卷系列答案
【题目】收入是衡量一个地区经济发展水平的重要标志之一,影响收入的因素有很多，为分析学历对收入的作用，某地区调查机构欲对本地区进行了此项调查.
（1）你认为应采用何种抽样方法进行调查？
（2）经调查得到本科学历月均收入条形图如图，试估算本科学历月均收入
的值？
（3）设学年为
，令
，月均收入为
，已知调查机构调查结果如下表
学历 （年） | 小学 | 初中 | 高中 | 本科 | 硕士生 | 博士生 |
| 6 | 9 | 12 | 16 | 19 | 22 |
| 2.0 | 2.7 | 3.7 | 5.8 | 7.8 | |
| 2210 | 2410 | 2910 |
| 6960 |
从散点图中可看出
和
的关系可以近似看成是一次函数图像. 若回归直线方程为
，试预测博士生的平均月收入.
