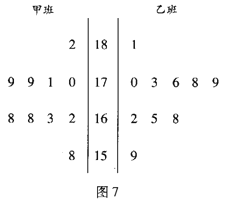
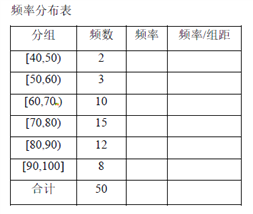
题目内容
【题目】已知函数f(x)=sin2x+sinx+cosx,以下说法中不正确的是( )
A.f(x)周期为2π
B.f(x)最小值为﹣ ![]()
C.f(x)在区间[0, ![]() ]单调递增
]单调递增
D.f(x)关于点x= ![]() 对称
对称
【答案】C
【解析】解:①∵f(x+2π)=sin[2(x+2π)]+sin(x+2π)+cos(x+2π)=sin2x+sinx+cosx=f(x),
∴函数周期为2π,故①正确;
②设t=sinx+cosx= ![]() sin(x+
sin(x+ ![]() )∈[﹣
)∈[﹣ ![]() ,
, ![]() ],
],
∴t2=(sinx+cosx)2=1+sin2x,
∴sin2x=t2﹣1,
∴y=sin2x+sinx+cosx=t2﹣1+t=t2+t﹣1=(t+ ![]() )2﹣
)2﹣ ![]() ,t∈[﹣
,t∈[﹣ ![]() ,
, ![]() ],
],
由二次函数可知,当t∈[﹣ ![]() ,﹣
,﹣ ![]() ]时,函数y=t2+t﹣1单调递减,当t∈[﹣
]时,函数y=t2+t﹣1单调递减,当t∈[﹣ ![]() ,
, ![]() ]时,函数y=t2+t﹣1单调递增,
]时,函数y=t2+t﹣1单调递增,
∴当t=﹣ ![]() 时,函数取最小值ymin=﹣
时,函数取最小值ymin=﹣ ![]() ,故②正确;
,故②正确;
③∵f(x)=sin2x+sinx+cosx,
当x= ![]() 时,f(x)=1+
时,f(x)=1+ ![]() ,
,
当x= ![]() 时,f(x)=1,
时,f(x)=1,
∴f(x)在区间[0, ![]() ]不是单调递增.
]不是单调递增.
故③错误;
④∵f( ![]() ﹣x)=sin[2(
﹣x)=sin[2( ![]() ﹣x)]+sin(
﹣x)]+sin( ![]() ﹣x)+cos(
﹣x)+cos( ![]() ﹣x)=sin(π﹣2x)+sinx+cosx=sin2x+sinx+cosx=f(x),
﹣x)=sin(π﹣2x)+sinx+cosx=sin2x+sinx+cosx=f(x),
∴函数关于x= ![]() 对称,故④正确.
对称,故④正确.
所以答案是:C.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目